Table of Contents
Zmiany w nieciągłych krokach
Pod koniec osiemnastego wieku, nauczyciel w niemieckiej szkole podstawowej chciał na dłużej zająć uczniów i zadał im nudne arytmetyczne zadanie. W uproszczeniu zadanie polegało na zsumowaniu wszystkich liczb od 1 do 100. Dzieci zaczęły pracować nad zadaniem a nauczyciel zapalił swoją fajkę pewien, że ma wolne do końca lekcji. Chwilę później, pewien chłopiec podał nauczycielowi odpowiedź: 5050. Nazywał się Carl Friedrich Gauss.
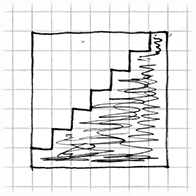
<center><i>Rys. 1.1. Dodawanie liczb od 1 do 7</i></center>
Rysunek 1.1 przedstawia jeden ze sposobów rozwiązania tego typu problemu. Zapełnione kolumny rysunku oznaczają liczby od 1 do 7. Zsumowanie ich jest równoznaczne ze znalezieniem pola powierzchni zacienionego obszaru. W przybliżeniu połowa kwadratów jest zacieniona, więc gdybyśmy chcieli przybliżone rozwiązanie, moglibyśmy po prostu obliczyć <latex> 7^{2}/2 = 24,5}\; </latex> . Ale, co pokazano na rysunku 1.2, uzyskanie dokładnego wyniku nie jest dużo trudniejsze. Jest siedem ząbków wystających poza przekątną. Ich sumaryczne pole wynosi <latex>\frac{7}{2}</latex> a więc pole powierzchni całego zacienionego obszaru wynosi <latex>(7^{2} + 7)/2 = 28</latex>. Ogólnie, suma pierwszych n liczb wynosi<latex>(n^2 + n)/2</latex>, co wyjaśnia wynik Gaussa: <latex>(100^2 + 100)/2 = 5050</latex>.
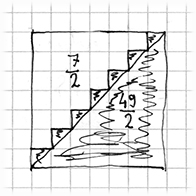
<center><i>Rys. 1.2. Dodawanie liczb od 1 do 7</i></center>
Dwie strony medalu
Podobne problemy pojawiają się bardzo często. Wyobraźcie sobie, że każdy dom w pewnym małym mieście generuje 1 tonę śmieci na wysypisku rocznie. Czas płynie a sterta śmieci na wysypisku rośnie. Oznaczmy lata jako n = 1, 2, 3, …, a funkcję x(n) oznaczającą ilość śmieci, które zebrały się na wysypisku pod koniec roku n. Jeżeli populacja wioski jest stała, na przykład 13 domów, to szybkość gromadzenia się śmieci na wysypisku jest stała i mamy x(n) = 13n.
Co w wypadku, gdy populacja miasta rośnie? Jeśli populacja miasta równa się 1 domowi w 1 roku i rośnie do dwóch domów rok później itd., mielibyśmy ten sam problem, który młody Gauss rozwiązał. Po 100 latach, ilość zgromadzonych śmieci będzie równa właśnie 5050 tonom. Sterta śmieci rośnie coraz bardziej co roku; prędkość zmiany x nie jest stała. Tabelaryzując:
| szybkość zmian | ilość zgromadzonych śmieci | |
|---|---|---|
| 13 | 13n | |
| n | <latex>(n | 2 + n)/2</latex> |
Szybkość zmiany naszej funkcji x może zostać zapisana jako <latex>\.{x}</latex>. Mając funkcję <latex>\.{x}</latex>, możemy zawsze wyznaczyć funkcję x dla każdej wartości n obliczając łączną sumę.
Podobnie, jeśli znamy x możemy wyznaczyć <latex>\.{x}</latex> poprzez odejmowanie. W przypadku, gdy x = 13n, możemy znaleźć <latex>\.{x} = x(n) - x(n - 1) = 13n - 13(n - 1) = 13</latex>. Lub, jeśli wiedzielibyśmy że zgromadzona ilość śmieci była określona przez <latex>(n^2 + n)/2</latex>, moglibyśmy obliczyć populację miasta poprzez:
<latex>
$ \begin{equation*}
\frac{n^2 + 2}{2} - \frac{(n-1)^2 + (n - 1)}{2} = \frac{n^2 + n - (n^2 - 2n +1 +n -1)}{2} = n
\end{equation*}
$
</latex>
<plot> set xtics axis nomirror set ytics axis nomirror set samples 160 set zeroaxis
set xrange [ 0.00000 : 7.00000 ] noreverse nowriteback set yrange [ 0.00000 : 30.00000 ] noreverse nowriteback set zeroaxis
plot x + 1/2, (x*x+x)/2 </plot>
<center><i>Rys. 1.3. x' to nachylenie k</i></center>
Graficzna interpretacja powyższego jest przedstawiona na rysunku 1.3: na wykresie <latex>x = (n^2 + n)/2</latex>, nachylenie linii łączącej dwa kolejne punkty to wartość funkcji <latex>\.{x}</latex>.
Innymi słowy, funkcje x i <latex>\.{x}</latex> są jakby różnymi stronami tego samego medalu. Jeśli znasz jedną, możesz znaleźć drugą - z dwoma zastrzeżeniami.
Po pierwsze, dotychczas zakładaliśmy, że funkcja x zaczyna się w x(0) = 0. To nie jest zawsze prawda. Na przykład, gdybyśmy wlewali wodę do zbiornika przez pewien okres czasu, zbiornik prawdopodobnie nie był początkowo zupełnie pusty. W ten sposób, jeżeli znamy <latex>\.{x}</latex>, nie możemy znaleźć wszystkiego o funkcji x bez jakichś dalszych informacji: wartości początkowej x. Jeśli ktoś powie nam, że <latex>\.{x} = 13</latex>, nie możemy z tego wyciągnąć wniosku, że x = 13n, ale że x = 13n + c, gdzie c to jakaś stała. Nie ma takich niejasności, jeśli idziemy w drugą stronę, to jest od x do <latex>\.{x}</latex>. Nawet jeśli <latex>x(0)\neq 0</latex>, dalej mamy <latex>\.{x} = 13n + c - [13(n-1) + c] = 13</latex>.
Po drugie, może być trudne, lub nawet niemożliwe, by znaleźć odpowiednią formułę by obliczyć łączną sumę x, mając formułę na szybkość zmiany <latex>\.{x}</latex>. Gauss miał przebłysk geniuszu, dzięki któremu otrzymał wcześniejsze <latex>(n^2 + n)/2</latex>, ale ogólnie często tylko za pomocą komputera będziemy mogli obliczyć liczbę dla łącznej sumy, a nie wzór, który byłby poprawny dla każdej wartości n.
Zgadywanki
Nawet jeśli brak nam geniuszu Gaussa, możemy rozpoznać pewne wzorce. Jednym jest to, że jeśli <latex>\.{x}</latex> jest funkcją, która stale się zwiększa, wydaje się, że x będzie funkcją, która rośnie jeszcze szybciej. W przypadku <latex>\.{x} = n</latex> i <latex>x = (n^2 + n)/2</latex> rozważmy, co się stanie dla dużych wartości n, jak na przykład 100. Dla tej wartości n, <latex>\.{x} = 100</latex>, ale nawet nie wyciągając kalkulatora widzimy, że x będzie znacznie większe.
Wszystkie funkcje x i <latex>\.{x}</latex>, które dotychczas widzieliśmy, były wielomianami. Jeśli x jest wielomianem, to możemy również znaleźć wielomian dla <latex>\.{x}</latex>, ponieważ jeśli x jest wielomianem, to x(n) - x(n - 1) również nim będzie. Wszystko wskazuje na to, że każdy wielomian, który moglibyśmy wybrać dla <latex>\.{x}</latex> mógłby również odpowiadać x, który jest wielomianem. Widać również, że jest tu pewien schemat związany z potęgą n. Przypuśćmy, że x jest wielomianem a najwyższa potęga n w tym wielomianie to pewna liczba - rząd(? order) wielomianu. Wtedy <latex>\.{x}</latex> jest wielomianem tego rzędu minus jeden. Łatwo to udowodnić w kierunku x do <latex>\.{x}</latex>, ale dużo trudniej jest udowodnić, że jeśli <latex>\.{x}</latex> jest wielomianem pewnego rzędu, to x również jest wielomianem tego rzędu plus jeden.
Wyobrażalibyśmy sobie wtedy, że łączna suma <latex>\.{x} = n^2</latex> byłaby wielomianem rzędu 3. Jeżeli obliczymy <latex>x(100) = 1^2 + 2^2 + … + 100^2</latex> na komputerze, otrzymamy liczbę 338350, która wygląda podejrzanie podobnie do 1000000/3. Wygląda na to, że <latex>x(n) = n^3/3 + …</latex>, gdzie kropki oznaczają wyrazy związane z niższymi potęgami n, jak na przykład <latex>n^2</latex>.
Ciągła zmiana
Zauważyliście, że podstępnie umieściłem coś w przykładzie napełniającego się zbiornika? Funkcje x i <latex>\.{x}</latex>, których używałem jako przykładów, zawsze były zdefiniowane na liczbach całkowitych, aby prezentowały zmianę, która następuje w dyskretnych krokach, ale przepływ wody do zbiornika jest przecież płynny i ciągły. Czy aby na pewno? Woda składa się przecież z molekuł. Molekuły wody są jednak tak małe, że nie widzimy ich jako osobnych jednostek. Wykres na rysunku 1.4 jest dyskretny, ale wygląda prawie jak ciągły, z powodu skali przyjętej tak, że punkty zlewają się w jedno.
<plot> unset border set xtics ( 0, 10, 20, 30) axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -0.50000 : 30.00000 ] noreverse nowriteback set yrange [ -0.50000 : 500.00000 ] noreverse nowriteback set zeroaxis
plot x*x/2 with points
</plot>
<center><i>Rys. 1.4. Przy takiej skali, funkcja wydaje się prawie ciągła</i></center>
Tym samym tropem podążał fizyk, Izaak Newton, w latach sześćdziesiątych XVII wieku i znalazł sposób analizy funkcji x i <latex>\.{x}</latex>, które były ciągłe. Zapis <latex>\.{x}</latex> to jego zasługa (a korzystał z niego tylko dla funkcji ciągłych). Te matematyczne metody nazywamy dzisiaj rachunkiem różniczkowym i całkowym.
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -0.50000 : 2.00000 ] noreverse nowriteback set yrange [ -0.50000 : 2.00000 ] noreverse nowriteback set zeroaxis
plot x*x/2, x - 0.5
</plot>
<center><i>Rys. 1.5. Funkcja x(t) i styczna do niej w punkcie P(1;0,5)</i></center>
Newton był fizykiem i ów rachunek był mu potrzebny do badań nad ruchem ciał. Jeżeli ciało porusza się w jednym wymiarze, możemy określić jego pozycję zmienną x, x będzie wtedy funkcją czasu, t. Prędkość zmiany pozycji ciała <latex>\.{x}</latex> to jego prędkość. Wczesne eksperymenty Galileusza wykazały, że gdy kula staczała się z równi pochyłej, jej pozycja była proporcjonalna do <latex>t^2</latex>, więc Newton wywnioskował, że wykres 1.5 byłby typowym dla każdego ciała poruszającego się pod wpływem stałej siły (na przykład <latex>7t^2</latex>, <latex>\frac{t^2}{42}</latex> lub cokolwiek innego, proporcjonalnego do <latex>t^2</latex>, zależnie od siły działającej na ciało i jego masy).
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -0.50000 : 2.00000 ] noreverse nowriteback set yrange [ -0.50000 : 2.00000 ] noreverse nowriteback set zeroaxis
plot x*x/2, 3*x - 0.5
</plot>
<center><i>Rys. 1.6. Ta prosta nie jest styczna do funkcji, przecina ją</i></center>
Ponieważ funkcje te są ciągłe a nie dyskretne, nie możemy definiować związku pomiędzy x a <latex>\.{x}</latex> twierdząc, że x to łączna suma <latex>\.{x}</latex>'ów, lub że <latex>\.{x}</latex> to różnica pomiędzy dwoma kolejnym x'ami. Ale znaleźliśmy geometryczny związek pomiędzy dwoma dyskretnymi funkcjami i to może posłużyć nam jako definicja dla funkcji ciągłych: x to pole powierzchni pod wykresem funkcji <latex>\.{x}</latex>, lub innymi słowy <latex>\.{x}</latex> to nachylenie stycznej prostej na wykresie funkcji x. Skupimy sie na tym drugim.
Linia styczna definiowana jest jako linia przechodząca przez wykres w danym punkcie, ale w odróżnieniu do prostej pokazanej na rysunku 1.6, nie przecina go. Mierząc linijką wykres z rysunku 1.5 stwierdzamy, że nachylenie prostej jest bardzo bliskie 1, więc <latex>\.{x}(1) = 1</latex>. By to udowodnić, utwórzmy funkcję reprezentującą tą prostą: <latex>l(t) = t - 1/2</latex>. Chcemy udowodnić, że ta linia nie krzyżuje się z wykresem funkcji <latex>x(t) =\frac{t^2}{2}</latex>. Różnicą pomiędzy tymi dwiema funkcjami, x - l, jest wielomian <latex>\frac{t^2}{2} - t + \frac{1}{2}</latex>. Ten wielomian będzie równy 0 dla każdej wartości t, gdzie prosta dotyka lub krzyżuje się z krzywą. Możemy użyć wzoru kwadratowego by znaleźć te punkty a wynik pokaże, że istnieje tylko jeden, t = 1. Ponieważ x - l jest dodatnia dla co najmniej kilku punktów na prawo i na lewo od t = 1, musi być zawsze dodatnia, co oznacza, że linia zawsze leży pod krzywą, nigdy się z nią nie krzyżując.
Pochodna
To dowodzi temu, że <latex>\.{x}(1) = 1</latex>, ale zajęło to sporo czasu a nie chcemy tego robić aby określić <latex>\.{x}</latex> dla każdej wartości t. Istnieje pewien sposób by tego uniknąć i znaleźć wzór funkcji <latex>\.{x}</latex>. Porównajcie wykresy na rysunkach 1.5 i 1.7. Oba są wykresami tej samej funkcji i obydwa wyglądają tak samo. Czym się różnią? Jedyną różnicą jest skala, na rysunku 1.7 oś t została podzielona przez 2 a oś x przez 4. Wykres wygląda tak samo, ponieważ podwojenie t mnoży <latex>\frac{t^2}{2}</latex> przez cztery. Linia styczna w tym wypadku to linia t = 2, a nie t = 1 i pomomo tego, że wygląda tak samo jak na rysunku 1.5, nią nie jest, z powodu różnych skali. Linia z rysunku 1.5 miała nachylenie równe 1/1 = 1, a ta z rysunku 1.7 4/2 = 2. To oznacza, że <latex>\.{x}(2) = 2</latex>. Ogólnie, przykład ze zmianą skal pokazuje, że <latex>\.{x}(t) = t</latex> dla każdego t.
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -0.50000 : 4.00000 ] noreverse nowriteback set yrange [ -0.50000 : 8.00000 ] noreverse nowriteback set zeroaxis
plot x*x/2, 2*x - 2
</plot>
<center><i>Rys. 1.7. Ponownie funkcja t^2/2. Czy różni się od rysunku 1.5? </i></center>
To nazywa się różniczkowaniem: znajdywaniem wzoru dla funkcji <latex>\.{x}</latex>, zakładając, że mamy wzór funkcji x. Funkcja <latex>\.{x}</latex>(lub x') jest nazywana pochodną funkcji x. Proces odwrotny, tj. określenie wzoru x na podstawie wzoru <latex>\.{x}</latex> nazywa się całkowaniem.
Zauważcie podobieństwo pomiędzy wynikami dla ciągłych funkcji <latex>x = \frac{t^2}{2}\quad \.{x} = t</latex> a wcześniejszymi wynikami dla funkcji dyskretnych: <latex>x =\frac{n^2 + n}{2}\quad \.{x} = n</latex>.
Podobieństwo to nie przypadek. Funkcja ciągła jest to po prostu wygładzona wersja funkcji dyskretnej. Na przykład, ciągła wersja funkcji schodkowej, pokazanej na rysunku 1.2 wyglądałaby jak trójkąt, bez wystających zębów; pole powierzchni tych zębów jest reprezentowane przez składnik <latex>\frac{n}{2}</latex> wyniku dyskretnego <latex>x = \frac{n^2 + n}{2}</latex>, co jest jedyną różnicą od wyniku ciągłego <latex>x = \frac{t^2}{2}</latex>.
Własności pochodnej
(1) Z definicji pochodnej bezpośrednio wynika, że mnożąc funkcję przez stałą pomnaża jej pochodną przez tą samą stałą. Skoro wiemy, że pochodna <latex>\frac{t^2}{2}</latex> to t, możemy szybko określić pochodną <latex>t^2</latex> równą 2t a pochodna <latex>\frac{t^2}{17}</latex> wynosi <latex>\frac{2t}{17}</latex>.
(2) Jeśli dodamy dwie funkcje, ich pochodne się dodają. Dobrym przykładem na to jest t: pochodną t jest 1, ponieważ x = t to linia z nachyleniem równym 1 a linia styczna leży na tej pierwszej.
<box 90% |Analitycznie:>
<latex> $ \begin{equation*} \frac{d(y+z)}{dx} = \frac{dy}{dx} + \frac{dz}{dx} \end{equation*} $ </latex>
ponieważ:
<latex> $ \begin{equation*} \frac{d(y + z)}{dx} = \lim_{h = 0} \frac{[f(x + h) + g(x + h)] - [f(x) + g(x)]}{h} =
\end{equation*} $ </latex> <latex> $ \begin{equation*} \lim_{h = 0} \frac{f(x + h)-f(x)}{h} + \lim_{h = 0} \frac{g(x + h) - g(x)}{h} = \end{equation*} $ </latex> <latex> $ \begin{equation*} \frac{dy}{dx} + \frac{dz}{dx} \end{equation*} $ </latex>
</box>
(3) Pochodna stałej jest równa zeru, ponieważ wykres funkcji stałej to pozioma linia z nachyleniem równym zeru. <box 90% |Analitycznie:>Niech funkcja f ma wartość stałą: <latex>f(x) = c</latex>. Wtedy <latex>\frac{dc}{dx} = 0</latex> ponieważ <latex>f(x + h) = c = f(x)</latex>, skąd <latex>\[\lim_{h = 0} \frac{f(x + h) - f(x)}{h} = 0\]</latex></box>
Wiemy już wystarczająco dużo aby różniczkować trudniejsze wielomiany.
++++ Przykład 1. | Pochodna <latex>5t^2 + 2t</latex> to pochodna <latex>5t^2</latex> plus pochodna <latex>2t</latex>, ponieważ pochodne się dodają. Pochodna <latex>5t^2</latex> to pochodna <latex>t^2</latex>, pomnożona przez 5, a pochodna 2t to podwojona pochodna t. Łącząc to wszystko razem otrzymujemy: <latex>(5)(2t) + (2)(1) = 10t + 2</latex>. ++++
++++ Przykład 2. | Owad ze Stanów Zjednoczonych jest przypadkowo wypuszczony w chińskiej wiosce. Owady rozprzestrzeniają się z prędkością s kilometrów na rok, tworząc poszerzające się koło. Znajdź liczbę kilometrów kwadratowych na rok nowo zainfekowanych obszarów. Sprawdź jednostki wyniku.
Niech t będzie czasem w latach, od którego owady zostały wypuszczone. Promień koła równa się r = st, a jego pole wynosi <latex>a = \pi r^2 = \pi (st)^2</latex>. Aby przedstawić to w postaci wielomianu, msimy przepisać to jako <latex>a = (\pi s^2)t^2</latex>. Pochodna wynosi: <latex>\.{a} = (2\pi s^2)t</latex>. Jednostką s są km/rok, potęgując je mamy <latex>km^2/rok^2</latex>. 2 i <latex>\pi</latex> są bezjednostkowe, a mnożąc przez t otrzymujemy jednostkę <latex>km^2/rok</latex>, co jest tym, czego się spodziewamy dla <latex>\.{a}</latex>.
Interpretując wyniki, zauważamy kilka rzeczy. Po pierwsze, prędkość rozprzestrzeniania się owadów nie jest stała lecz proporcjonalna do t - im szybciej zabierzemy się za walkę z owadami tym łatwiej będzie to zrobić. Po drugie, zauważamy, że wynik jest proporcjonalny do <latex>s^2</latex>. To wskazuje na to, że cokolwiek spowoduje zmniejszenie promienia koła s będzie bardzo pomocne - zmniejszenie s o połowę zmniejszy <latex>\.{a}</latex> poczwórnie. ++++
Wielomiany wyższych rzędów
Dotychczas nasze wyniki pochodnych wielomianów wyglądają następująco:
| funkcja | pochodna | |
|---|---|---|
| 1 | 0 | |
| t | 1 | |
| <latex>t | 2</latex> | 2t |
Interpretując 1 jako <latex>t^0</latex>, możemy zauważyć ogólną regułę, która mówi, że pochodna od <latex>t^k</latex> wynosi <latex>kt^{k - 1}</latex>. Dowód powyższego jest prosty ale niezbyt oświecający, jeśli wykorzystalibyśmy dotychczasowo używane metody.
Druga pochodna
Opisałem, jak Galileusz i Newton odkryli, że ciało, na które zaczyna działać zewnętrzna siła, miałoby prędkość <latex>\.{x}</latex>, która jest proporcjonalna do t i położenie x. Stała proporcjonalna dla prędkości jest nazywana przyspieszeniem, a, więc <latex>\.x = at</latex> oraz <latex>x = \frac{at^2}{2}</latex>. Przykładowo, samochód przyspieszający od znaku stopu miałby duże przyspieszenie a jego prędkość w danym okresie czasu byłaby dużą liczbą. Przyspieszenie można uznawać jako pochodną pochodnej x, zapisywaną jako <latex>\ddot{x}</latex>, z dwiema kropkami. W naszym przykładzie <latex>\ddot{x} = a</latex>. Generalnie, przyspieszenie nie musi być stałe. Samochód w końcu będzie musiał przestać przyspieszać.
++++ Przykład 4. | Przypuśćmy, że pilot sterowca właśnie włączył silnik, który wprawie w ruch śmigło, które porusza się w górę. Siła wynikowa na sterowiec jest więc rosnąca, dzięki czemu sterowiec otrzymał przyspieszenie <latex>\ddot{x} = 3t</latex>, które rośnie z czasem. Znaleźć prędkość i położenie sterowca jako funkcje czasu.
W przypadku prędkości, potrzebujemy wielomianu, którego pochodną jest 3t. Wiemy, że pochodną <latex>t^2</latex> jest 2t, więc potrzebujemy funkcji większej o 3/2: <latex>\dot{x} = \frac{3}{2}t^2</latex>. Moglibyśmy do tego dodać jakąkolwiek stałą otrzymując: <latex>\dot{x} = \frac{3}{2}t^2 + 14</latex>, gdzie 14 byłoby prędkością początkową sterowca. Ale skoro sterowiec był początkowo nieruchomy, możemy założyć, że prędkość początkowa wynosiła zero.
W przypadku położenia, potrzebujemy czegoś, czego pochodną jest <latex>\frac{3}{2}t^2</latex>. Pochodną od <latex>t^3</latex> jest <latex>3t^2</latex>, więc potrzebujemy czegoś równego połowie: <latex>x = \frac{t^3}{2}</latex>. ++++
Druga pochodna może być interpretowana jako miara krzywizny wykresu funkcji, jak to pokazano na rysunku 1.8. Wykres funkcji x = 2t jest prostą bez krzywizny. Jego pierwsza pochodna to 2 a druga zero. Funkcja <latex>t^2</latex> ma drugą pochodną równą 2, a o dużo bardziej ciasnej krzywiźnie funkcja <latex>7t^2</latex> ma większą drugą pochodną, 14.
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -2.00000 : 2.00000 ] noreverse nowriteback set yrange [ -0.50000 : 8.00000 ] noreverse nowriteback set zeroaxis
plot 7*x*x, x*x, 2*x
</plot>
<center><i>Rys. 1.8. Wykresy funkcji 2t, t^2 i 7t^2</i></center>
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -2.00000 : 2.00000 ] noreverse nowriteback set yrange [ -0.50000 : 4.00000 ] noreverse nowriteback set zeroaxis
plot x*x, 3 - x*x
</plot>
<center><i>Rys. 1.9. Funkcje t^2 i 3 - t^2</i></center>
Znak drugiej pochodnej oznacza wklęsłość. Na rysunku 1.9 funkcja <latex>t^2</latex> jest wklęsła ku górze co odpowiada znakowi dodatniemu drugiej pochodnej. Druga pochodna funkcji <latex>3-t^2</latex> jest ujemna, więc funkcja jest wklęsła ku dołowi.
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -2.00000 : 2.00000 ] noreverse nowriteback set yrange [ -8.00000 : 8.00000 ] noreverse nowriteback set zeroaxis
plot x*x*x
</plot>
<center><i>Rys. 1.10. Funkcja t^3 ma punkt przegięcia w t = 0</i></center>
Wykres na rysunku 1.10 to trzecia możliwość. Funkcja <latex>t^3</latex> ma pochodną równą <latex>3t^2</latex>, która równa się zeru dla t = 0. Ten punkt nazywa się punktem przegięcia. Wypukłość wykresu jest ku dołowi na lewo a ku górze na prawo. Punkt przegięcia to miejsce, gdzie funkcja zmienia wypukłość z jednej w drugą.
Zastosowanie
Maksima i minima
Gdy funkcja rośnie, zakręca i zaczyna maleć, na szczycie funkcji posiada nachylenie równe zeru. Punkt, w którym <latex>\.{x} = 0</latex> mógłby oznaczać miejsce, gdzie x byłoby maksymalne. Z drugiej strony, gdyby wypukłość tej funkcji była odwrotna, w punkcie tym byłoby minimum funkcji.
++++ Przykład 5. | Fred otrzymał tajemniczy e-mail ze wskazówką mówiącą, że jego inwestycje w pewnym kapitale akcyjnym będą miały wartość określoną przez <latex>x = -2t^4 + (6.4577*10^10)t</latex>, gdzie t >= 2005 to rok. Kiedy powinien sprzedać akcje?
Jeżeli funkcja osiągnie w pewnym punkcie maksimum, to pochodna powinna być równa zeru:
<latex>
0 = -8t^3 + 6.4577*10^{10}\\
t = (\frac{6.4577*10^{10}}{8})^{\frac{1}{3}}\\
t = \pm 2006.0
</latex>
Oczywiście rozwiązanie t = -2006,0 jest nieprawidłowe - giełda aż tak stara nie jest. Pozostaje wynik 2006,0. Czy Fred powinien w takim razie na początku roku 2006 sprzedać akcje? Ekstremum w t = 2006 może być maksimum, minimum lub punktem przegięcia. Fred z całą pewnością nie chce sprzedawać akcji w t = 2006, gdyby to było minimum. By sprawdzić, która to możliwość, obliczamy drugą pochodną: <latex>\ddot{x} = -24t^2</latex>. Podstawiając t = 2006, widzimy, że druga pochodna dla tego t jest ujemna, co oznacza w tym punkcie maksimum. Sprzedajemy!
++++
Podczas tych rozważań, zakładaliśmy, że maksimum lub minimum jest tam(?), gdzie funkcja jest gładka. Są inne możliwości. Na rysunku 1.11, minimum funkcji występuje na końcu swojej dziedziny.
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -1.00000 : 2.00000 ] noreverse nowriteback set yrange [ -0.50000 : 2.00000 ] noreverse nowriteback set zeroaxis
plot sqrt(x)
</plot>
<center><i>Rys. 1.11. Funkcja x = sqrt(t) ma minimum w t = 0, co nie jest punktem, m, w którym pierwsza pochodna jest równa zeru. Ten punkt jest brzegiem dziedziny funkcji</i></center>
<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -1.00000 : 1.00000 ] noreverse nowriteback set yrange [ -0.50000 : 2.00000 ] noreverse nowriteback set zeroaxis
plot abs(x)
</plot>
<center><i>Rys. 1.12. Funkcja x = |t| ma minimum w t = 0, co nie jest miejscem, gdzie pochodna funkcji jest równa zeru. To miejsce, gdzie funkcja nie jest różniczkowalna</i></center>
Inna możliwość to istnienie maksimum i minimum danej funkcji w pewnym punkcie, w którym jej pochodna nie jest dobrze zdefiniowana, co pokazane jest na rysunku 1.12. W t = 0 jest zgięcie, więc duża liczba prostych mogłaby być poprowadzona przez wykres, pozostając po jednej jego stronie. Nie ma jednej, unikalnej stycznej, więc pochodna jest nieokreślona.
++++ Przykład 6. | Rolnik Andrzej posiada ogrodzenie o długości L, za pomocą którego chce ogrodzić prostokątną działkę. Udowodnij, że ogrodzi największy obszar, formując kwadrat o boku równym L/4.
Jeśli szerokość i długość prostokąta to t i u a Andrzej chce zużyć cały swój materiał, to obwód prostokąta, 2t + 2u równa się L, więc dla danej szerokości t, długość wynosi u = L/2 - t. Pole powierzchni wynosi a = tu = t(L/2 - t). Funkcja ma rzeczywisty sens tylko, gdy 0 ⇐ t ⇐ L/2, gdyż dla wartości t poza tym obszarem albo t albo u byłyby ujemne. Funkcja a(t) może przeto mieć maksimum albo w miejscu, gdzie <latex>\.{a} = 0</latex>, lub na brzegach dziedziny funkcji. Możemy wyeliminować drugą możliwość, ponieważ pole powierzchni na brzegach dziedziny wynosi zero. Aby określić pochodną, musimy najpierw przedstawić a jako wielomian: <latex>a = -t^2 + \frac{L}{2}t</latex>. Pochodna wynosi <latex>\.{a} = -2t + \frac{L}{2}</latex>. Przyrównując to do zera, znajdujemy <latex>t = \frac{L}{4}</latex>. To jest maksimum, a nie minimum lub punkt przegięcia, ponieważ druga pochodna jest stała: <latex>\ddot{a} = -2</latex> i ujemna dla każdej wartości t, włączając w to <latex>t = \frac{L}{4}</latex>. ++++
Rozchodzenie się (propagacja) błędów
WNBA (Women's National Basketball Assoc.) twierdzi, że piłki używane podczas gier ligowych powinny mieć promień równy 11.6cm, z dopuszczalną odchyłką plus/minus 0.1cm. Z jaką dokładnością możemy określić objętość piłki?
Równanie na objętość kuli wynosi <latex>V = (\frac{4}{3})\pi r^3 = 6538 cm^3 \approx 6,5l</latex>. Mamy funkcję V® i chcemy wiedzieć, jak wielki wpływ na wynik tej funkcji będzie miała zmiana promienia r o małą liczbę. Ponieważ liczba ta jest mała w stosunku do r, rozsądnym jest wykorzystanie stycznej jako przybliżenia faktycznego wykresu. Nachylenie stycznej to pochodna V i równa się <latex>4\pi r^2</latex> (to jest pole powierzchni piłki). Nastaw(? setting) (nachylenie) = (wzrost)/(bieg) a rozwiązując to na wzrost, który reprezentuje zmianę w objętości V, znajdujemy, że objętość może się różnić o <latex>(4\pi r^2)(0,1 cm) = 170 cm^3</latex>. Objętość piłki może zostać wyrażona jako <latex>6500\pm 170 cm^3</latex>, gdzie pierwotna liczba 6538 została zaokrąglona do najbliższej setki by uniknąć wrażenia, że 3 i 8 cokolwiek znaczą, gdyż możliwy błąd jest liczony w setkach.
Ta kalkulacja jest przykładem bardzo często pojawiającej się w nauce sytuacji, gdy opieramy obliczenia na liczbach, które zawierają w sobie pewną niepewność, tworząc pewną niepewność i w końcowym wyniku. Nazywa się to propagacją błędów. Ideą jest to, że pochodna pokazuje jak bardzo dane wejściowe funkcji wpływają na jej dane wyjściowe.
Powyższy przykład można również rozwiązać bez różniczki, obliczając objętość za pomocą promienia, który zwiększał się od 11.6 do 11.7 cm i znajdując różnicę pomiędzy tymi dwiema objętościami. Rozumiejąc to różniczkowo umożliwia nam głębsze zrozumienie istoty sprawy. Na przykład, zauważyliśmy że pochodna objętości to pole powierzchni piłki, co ułatwia wizualizację geometryczną - możemy wyobrazić sobie pompowaną piłkę, gdzie jej promień rośnie o milimetr. Ilość dodanej objętości równa się polu powierzchni piłki pomnożonej przez 1 milimetr.



