sqWiki

Matematycy znależli kilka różnych systemów logicznych do pracy z nieskończonością i w większości z nich nieskończoność przychodzi w różnych rozmiarach i “smakach”. Newton, jak i niemiecki matematyk Leibniz (który (podobno) niezależnie opracował rachunek różniczkowy) mieli silne intuicyjne przekonanie, że rachunek różniczkowy najbardziej związany był z nieskończenie małymi liczbami. Rozważmy liczbę <latex>1,1^2 = 1,21</latex>. Dwójka na pierwszym miejscu po przecinku jest taka sama jak dwójka, która widnieje we wzorze 2t pochodnej <latex>t^2</latex>.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ 0.60000 : 1.40000 ] noreverse nowriteback set yrange [ 0.60000 : 1.40000 ] noreverse nowriteback set zeroaxis

plot x*x, (2*x)-1 </plot> <center><i>Rys. 2.1. Zbliżenie na funkcję x = t^2, pokazujące linię łączącą punkty (1; 1) i (1,1; 1,21)</i></center>

Rysunek 2.1 pokazuje tę ideę. Linia łącząca (1;1) i (1,1;1,21) jest prawie nierozróżnialna od stycznej w tej skali. Jej nachylenie wynosi (1,21 - 1)/(1,1 - 1) = 2,1, co jest bardzo bliskie do nachylenia stycznej, które wynosi 2. To dobre przybliżenie, ponieważ punkty były blisko siebie, w odległości 0,1 na osi t.

Jeżeli potrzebowalibyśmy lepszego przybliżenia, moglibyśmy obliczyć 1,01 = 1,0201. Nachylenie linii łączącej punkty (1; 1) i (1,01; 1,0201) wynosi 2,01, co jest jeszcze dokładniejsze, bliższe nachyleniu stycznej.

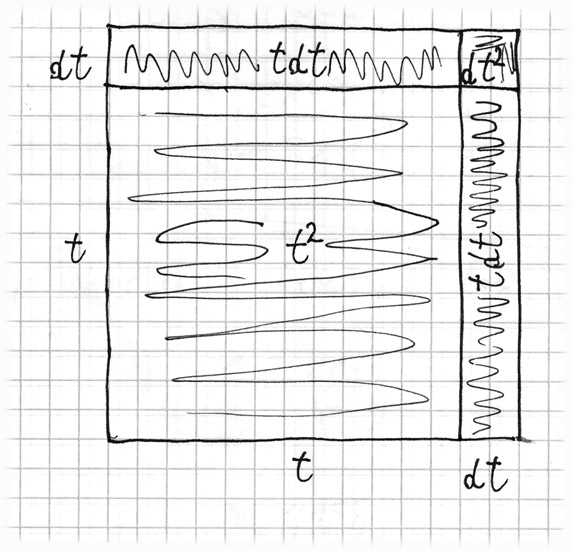
Inną metodą zobrazowania sobie tej idei jest to, że możemy zinterpretować <latex>x = t^2</latex> jako pole powierzchni kwadratu o boku długości t, jak pokazano na rysunku 2.2. Zwiększamy t o nieskończenie małą liczbę dt. To “d” to notacja Leibniza na bardzo małą różnicę (odczytywana jako de-te, pojedynczy symbol).

<center><i>Rys. 2.2. Geometryczne zobrazowanie pochodnej t^2</i></center>

Ideą jest to, że dt jest mniejsze niż każda inna liczba, którą moglibyśmy sobie wyobrazić, ale ciągle większa od zera. Pole powierzchni kwadratu zwiększa się o <latex>dx = 2tdt + dt^2</latex>, co jest analogiczne do skończonych liczb 0,21 i 0,0201, które obliczyliśmy wcześniej. Podczas gdy wcześniej dzieliliśmy przez skończoną zmianę w t 0,1 lub 0,01, teraz dzielimy przez dt, otrzymując <latex>\frac{dx}{dt} = \frac{2tdt + dt^2}{dt} = 2t + dt</latex> dla pochodnej. Na rysunku 2.1 dx/dt to nachylenie stycznej: zmiana x podzielona przez zmianę t.

Ale dodając nieskończenie małą liczbę dt do 2t nie zmieniamy jej o wielkość, która nawet teoretycznie byłaby mierzalna w rzeczywistości, więc odpowiedź właściwie wynosi 2t. Określając ją w t = 1, otrzymujemy dokładnie ten sam wynik, 2, do którego wcześniejsze przybliżone wyniki, 2,1 i 2,01 się zbliżały.

++++ Przykład 7. | By pokazać siłę nieskończenie małych wartości i notacji Leibniza, dowiedźmy że pochodna <latex>t^3</latex> to <latex>3t^2</latex>:

<latex> \frac{dx}{dt} = \frac{(t + dt)^3 - t^3}{dt} = \frac{3t^2dt + 3tdt^2 + dt^3}{dt} = 3t^2 + … </latex>

gdzie kropki wskazują na nieskończenie mały składnik, który możemy pominąć. ++++

Ten wynik wymagał sporo trudu i pomysłowości by go udowodnić metodami z rozdziału pierwszego. Stara metoda wymagałaby również zupełnie innego dowodu dla funkcji, która nie jest wielomianem, podczas gdy nową metodę możemy zastosować bardziej ogólnie, jak to zobaczymy w przykładach 8-10.

Łatwo jest popaść w błędne rozumowane, że nieskończenie małe liczby istnieją w jakimś magicznym świecie, gdzie nie możemy ich dotknąć. To może być prawdą w tym samym świecie, w którym nigdy w pełni nie zrozumiemy <latex>\sqrt{2}</latex>, ponieważ jego rozwinięcie dziesiętne biegnie w nieskończoność i nigdy nie możemy dokładnie go wyznaczyć. Ale w praktyce, to nie przeszkadza nam w pracy z <latex>\sqrt{2}</latex>. Wyznaczamy przybliżoną jego wartość, przykładowo 1,41. Nieskończenie małe liczby nie są mniej lub bardziej tajemnicze niż liczby nierzeczywiste a w szczególności, potrafimy je przedstawić na komputerze.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ 0.00000 : 6.00000 ] noreverse nowriteback set yrange [ -1.00000 : 1.00000 ] noreverse nowriteback set zeroaxis

plot sin(x), cos(x) </plot> <center><i>Rys. 2.3. Wykres funkcji sin(t) i jej pochodnej cos(t)</i></center>

++++ Przykład 8. | Pochodna x = sin(t), z t wyrażonym w radianach wynosi <latex>\frac{dx}{dt} = \frac{\sin{(t + dt)} - \sin{t}}{dt}</latex> a wiedząc, że <latex>\sin{\alpha + \beta} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}</latex> otrzymujemy <latex>\frac{\sin{t}\cos{dt} + \cos{t}\sin{dt} - \sin{t}}{dt}</latex>. Zakładając bardzo małe przybliżenia kąta <latex>\sin{u}\approx u</latex> oraz <latex>\cos{u}\approx 1</latex> mamy

<latex> \frac{dx}{dt} = \frac{\cos{tdt}}{dt} + … = \cos{t} + … </latex>

gdzie “…” to błąd spowodowany przybliżeniem bardzo małego kąta. ++++

To w zasadzie wszystko odnośnie obliczania pochodnej, pomijając fakt, że nie dowiedliśmy, że przybliżenia małych kątów są wystarczająco dobre. W przykładzie 7, gdy obliczaliśmy pochodną <latex>t^3</latex>, wynikowe równanie współczynnika dx/dt wyszło w formie, w której mogliśmy zbadać składniki “…” i je sprawdzić zanim odrzuciliśmy je z tego powodu, że były znikome.

Rysunek 2.3 pokazuje wykresy funkcji i jej pochodnej. Zauważcie jak te dwa wykresy sobie odpowiadają. W t = 0, nachylenie sin(t) jest największe i dodatnie; w tym miejscu pochodna funkcji osiąga najwyższą dodatnią wartość 1. W <latex>t = \frac{\pi}{2}</latex>, sin(t) osiąga maksimum i ma nachylenie równe zeru; cos(t) jest tam równe zeru. W <latex>t = \pi</latex>, w środku wykresu, sin(t) ma największe ujemne nachylenie a cos(t) przyjmuje najniższą wartość -1.

Fizycznie, sin(t) mógłby oznaczać położenie wahadła gdy poruszało się w tę i z powrotem, od lewej do prawej a cos(t) oznaczałoby prędkość wahadła.

++++ Przykład 9. | Co z pochodną cosinusa? Cosinus i sinus tak naprawdę to ta sama funkcja, przesunięta w lewo lub prawo o <latex>\frac{\pi}{2}</latex>. Jeżeli pochodna sinusa jest taka sama jak on sam, tylko przesunięty w lewo o <latex>\frac{\pi}{2}</latex>, to pochodna cosinusa musi być cosinusem przesuniętym w lewo o <latex>\frac{\pi}{2}</latex>:

<latex> \frac{d\cos{t}}{dt} = \cos{(t + \frac{\pi}{2})} = -\sin{t} </latex> ++++

Następny przykład wymagać będzie drobnego podstępu. Do końca tego rozdziału poznacie ogólne metody rozwiązywania jakichkolwiek pochodnych bez potrzeby stosowania sztuczek.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -1.00000 : 1.00000 ] noreverse nowriteback set yrange [ 0.00000 : 3.00000 ] noreverse nowriteback set zeroaxis

plot 1/(1-x) </plot> <center><i>Rys. 2.4. Wykres funkcji x = 1/(1-t)</i></center>

++++ Przykład 10. | Znajdź pochodną 1/(1-t), określoną w t = 0.

Rysunek 2.4 pokazuje, jak wygląda ta funkcja. Dąży do nieskończoności w t = 1, ale dobrze się zachowuje w t = 0, gdzie ma dodatnie nachylenie. Dla dobrego zrozumienia, obliczmy kilka punktów na krzywej. Punkt, w którym różniczkujemy to (0; 1). Jeżeli określimy małą, dodatnią wartość t, możemy zaobserwować jak bardzo wynik się zwiększa względem 1 a to da nam przybliżenie dla pochodnej. Na przykład w t = 0,001, funkcja ma wartość 1,001001001001, więc pochodna jest w przybliżeniu (1,001 - 1)/(0.001 - 0) równa 1. Możemy więc przypuszczać, że pochodna jest równa dokładnie 1, ale to nie to samo co temu dowieść.

Spójrzmy jeszcze raz na liczbę 1,001001001001. Jest to wyraźnie liczba okresowa. Innymi słowy, widzimy że:

<latex> \frac{1}{1 - 1/1000} = 1 + \frac{1}{1000} + (\frac{1}{1000})^2 + … </latex>

a możemy z łatwością to sprawdzić mnożąc obie strony równania przez 1 - 1/1000 i zgrupować podobnie jak potęgi. To specjalny przypadek ciągu geometrycznego:

<latex> \frac{1}{1-t} = 1 + t + t^2 + … </latex>

który może zostać otrzymany poprzez sztuczny podział (? synthetic division) (ekwiwalent długiego podziału dla wielomianów (? polynomials long division), lub po prostu sprawdzony po sformułowaniu przypuszczenia opartego na liczbowym przykładzie powyżej, przez pomnożenie obu stron przez 1 - t.

Jak zobaczymy w podrozdziale 2 i jak ukrycie zakładaliśmy do tej pory, nieskończoności podlegają tym samym elementarnym prawom algebry jak rzeczywiste liczby, więc powyższa pochodna również utrzymuje się jako nieskończenie mała wartość t. Wynikiem pochodnej jest:

<latex> \frac{dx}{dt} = \frac{(1 + dt + dt^2 + …) - 1}{1 + dt - 1} = 1 + … </latex> ++++

Pomysł z nieskończenie małymi liczbami zawsze drażnił purystów. Jednym, z bardziej znaczących krytyków rachunku różniczkowego i całkowego był rówieśnik (sprawdzić na wikipedii) Newtona, George Berkeley, biskup Cloyne. Pomimo tego, że niektóre z jego zarzutów są zupełnie bezpodstawne (zaprzeczał możliwości drugiej pochodnej), krytyka pomysłu nieskończoności miała jakiś sens. Napisał sarkastycznie: “Nie są one ani skończonymi ilościami ani ilościami nieskończenie małymi ani właściwie niczym. Nie moglibyśmy nazywać ich duchami zmarłych ilości?” [Hahahahaha - przyp. tłum.]

Nieskończoności mogą wydawać się nieco straszne, ponieważ jeśli źle się z nim obchodzi, można udowodnić niedorzeczne rzeczy. Na przykład, powiedzmy że du będzie nieskończenie małe. Wtedy 2du jest również nieskończenie małe. Wtedy 1/du i 1/(2du) są równe nieskończoności, więc 1/du = 1/(2du). Mnożąc obie strony przez du, dowiedliśmy że 1 = 1/2.

W osiemnastym wieku, używanie nieskończenie małych liczb stało się jak cudzołóstwo: powszechnie praktykowane, lecz wstydliwe w kulturalnych kręgach. Ci, którzy z nich korzystali, nauczyli się paru reguł obchodzenia się z nimi. Przykładowo, znaleźliby wadę w dowodzie na 1 = 1/2, ponieważ założenie, że istnieje tylko jedna wielkość(?) nieskończoności, podczas gdy 1/du powinno być interpretowane jako nieskończoność dwukrotnie większa od 1/(2du). Użycie jednego symbolu, ∞, implikowało że nieskończoności posiadają tylko jeden rozmiar. Jednak praktykujący nieskończoności mieli sporo problemów jasno formułując reguły poprawnego ich użycia i nie mogli udowodnić, że logiczny, spójny system mógłby być wokół nich zbudowany.

W wieku dwudziestym, kiedy ja uczyłem się rachunku, osiągnięto konsensus, że nieskończenie małe wielkości nie są w ogóle liczbami. Zapisy typu dx/dt, jak mówił mój nauczyciel, to nie jest jedna liczba podzielona przez drugą, był to po prostu symbol oznaczający coś co nazywa się granicą, <latex>\lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}</latex>, gdzie Δx i Δt to skończone zmiany. Formalna definicja zostanie podana w podrozdziale 9, ale intuicyjnie koncepcja wygląda tak, że możemy otrzymać tak dobre przybliżenie do pochodnej jakie byśmy chcieli, zakładając że wybierzemy odpowiednio małe Δt.

To mnie usatysfakcjonowało do momentu, gdy dotarliśmy do tematu różniczkowania funkcji uwikłanej (implicit differentiation), gdzie kazano nam rozbić dx od dt, pozostawiając je po osobnych stronach równania. Po wykładzie, zapytałem nauczyciela, dlaczego teraz robi coś, czego wcześniej nie można było robić. Odpowiedział mi, że w istocie dx i dt to nie liczby, ale w większości wypadków można było ustrzec się błędów traktując je jako liczby i otrzymać poprawny wynik. “W większości wypadków!?” To wprowadziło mnie w zakłopotanie. Skąd mogłem wiedzieć, które wypadki należały do tej większości?

Ale, nieznany mi oraz mojemu nauczycielowi, matematyk Abraham Robinson w latach sześćdziesiątych wykazał, że można było konstruować spójny system liczb, który zawierał nieskończenie duże i nieskończenie małe liczby. Nazwał go systemem liczb hiperrealistycznych (?? Hyperreal number), a zawierał on liczby rzeczywiste jako podzbiór.

Ponadto, reguły mówiące o tym, co można a co nie z hiperrealistycznymi liczbami okazały się bardzo proste. Weźmy jakiekolwiek prawdziwe twierdzenie dotyczące liczb rzeczywistych. Załóżmy, że jest możliwe przekształcenie go w twierdzenie o “hiperrzeczywistych” w najbardziej oczywisty sposób, zamieniając słowo rzeczywiste w hiperrzeczywiste. Wtedy przekształcone twierdzenie w dalszym ciągu jest prawdziwe. To nazywa się zasadą przenoszenia (transfer principle).

Spójrzmy wstecz do mojego błędnego dowodu, że 1 = 1/2 w świetle tej prostej reguły. Końcowy krok tego wywodu jest całkowicie poprawny: mnożymy obie strony równania przez to samo. To twierdzenie, dotyczące liczb rzeczywistych, jest prawdziwe:

<box 60%>Dla każdej liczby rzeczywistej a, b i c, jeśli a = b, to ac = bc</box>

To może być przekształcone w oczywisty sposób w twierdzenie o hiperrzeczywistych liczbach:

<box 65%>Dla każdej liczby hiperrzeczywistej a, b i c, jeśli a = b, to ac = bc</box>

Jednakże, co z twierdzeniem, że 1/du i 1/(2du) równe są nieskończoności, więc są sobie równe? To nie jest przekształcenie twierdzenia, które jest prawdziwe dla liczb rzeczywistych, więc nie ma powodu by przypuszczać, że będzie prawdziwe w przypadku liczb hiperrzeczywistych - a właściwie, to jest błędne.

To co mówi nam zasada przenoszenia, to to że liczby rzeczywiste, jak zwykle myślimy, nie są wyjątkiem w przestrzeganiu zwykłych zasad algebry. Są zupełnie inne systemy liczb, jak na przykład hiperrzeczywiste, które również ich przestrzegają.

Czym więc liczby hiperrzeczywiste różnią się od rzeczywistych, skoro wszystko co prawdziwe dla jednych, jest również prawdziwe dla drugich? Należy pamiętać, że zasada przenoszenia nie gwarantuje, że każde twierdzenie o liczbach rzeczywistych może zostać przekształcone w twierdzenie o liczbach hiperrzeczywistych w najprostszy sposób, zastępując słowo “rzeczywiste” słowem “hiperrzeczywiste”. Poniżej twierdzenie, które jest prawdziwe dla liczb rzeczywistych, ale nie może być przekształcone tym sposobem: <box 80%>Dla każdej liczby rzeczywistej a, istnieje liczba całkowita n, która jest większa od a</box>

To twierdzenie nie może być przekształcone tak łatwo, ponieważ odwołuje się do podzbioru liczb rzeczywistych, nazywanego liczbami całkowitymi. Być może istnieje jakiś sposób przekształcenia, ale to wymagałoby nagłego olśnienia czy głębokiego zrozumienia problemu. Zasady przenoszenia nie można zastosować z tym twierdzeniem, ponieważ zbiór liczb hiperrzeczywistych posiada liczby nieskończone, które są większe od wszystkich liczb całkowitych. Sprzeczność w tym twierdzeniu może wyjaśnić nam, dlaczego liczby hiperrzeczywiste są tak wyjątkowe i różniące się od liczb rzeczywistych: zakładamy, że jest przynajmniej jedna hiperrzeczywista liczba, H, która jest większa od wszystkich liczb całkowitych.

Analogicznie do życia codziennego, porównaj następujące twierdzenia o studentach liceum, do którego uczęszczałem:

1. Każdy student mojego liceum posiadał parę oczu i twarz.
2. Każdy student mojego liceum, który był drużynie piłkarskiej był kretynem.

Przetłumaczmy je w twierdzenia o populacji Kalifornii. Studenci mojego liceum to jakby zbiór liczb rzeczywistych a obecna populacja Kalifornii to liczby hiperrzeczywiste. Twierdzenie 1 może być przekształcone bezmyślnie w twierdzenie, że każdy Kalifornijczyk posiada parę oczu i twarz; zamieniamy po prostu “każdy Kalifornijczyk” z “każdy student mojego liceum”. Ale twierdzenie 2 nie jest już tak proste, ponieważ odwołuje się do podzbioru studentów, którzy byli w drużynie piłkarskiej i nie jest oczywiste jaki miałby być tego odpowiednik w zbiorze Kalifornijczyków. Twierdzenie 2 to przykład twierdzenia, do którego zasada przenoszenie nie działa.

++++ Przykład 11 | Jako nietrywialny przykład zastosowania zasady przenoszenia, rozważmy jak pracować z wyrażeniami jak to, które pojawiło się, gdy chcieliśmy różniczkować <latex>t^2</latex> za pomocą nieskończenie małych liczb:

<latex> \frac{d(t^2)}{dt} = 2t + dt </latex>

Uzasadniłem wcześniej, że 2t + dt jest tak bliskie 2t, że dla wszystkich praktycznych zastosowań rozwiązaniem jest właśnie 2t. Ale czy jest poprawnym, twierdzenie że 2t + dt jest taką samą liczbą hiperrzeczywistą jak 2t? Nie. Możemy zastosować zasadę przenoszenia do następującego twierdzenia o liczbach rzeczywistych:

<box 80%>Dla każdej liczby rzeczywistej a lub b, zakładając że <latex>b\neq 0,\quad a+b\neq a</latex></box>

Ponieważ dt nie jest równe zeru, <latex>2t + dt \neq 2t</latex> ++++

Bardziej ogólnie, przykład 11 prowadzi do zobrazowania sobie każdej liczby otoczonej przez “aureolę” (?) liczb, które nie się jej nie równają, ale różnią się od niej tylko o nieskończenie małą ilość. Jest to podobne do idei, że każda liczba całkowita jest otoczona przez kilka ułamków, które można by do niej zaokrąglić. Moglibyśmy zdefiniować standardową część skończonej liczby hiperrzeczywistej, co oznacza że unikalna liczba rzeczywista różni się od niej nieskończenie mało. Przykładowo, standardowa część 2t + dt, zapisana jako st(2t + dt) równa się 2t. Pochodna fukcji powinna być zdefiniowana jako standardowa część dx/dt ale częściej piszemy dx/dt mając na myśli pochodną i nie martwimy się o różnice.

Jedną z rzeczy, których biskup Berkley nie lubił w nieskończenie małych liczbach to idea, że istniały one w pewnej hierarchii, z <latex>dt^2</latex> będącym nie tylko nieskończenie małym, ale również nieskończenie małym w porównaniu do nieskończenie małego dt. Jeśli dt jest przykładowo pchłą na psie, to <latex>dt^2</latex> jest mikroskopijną pchłą na pchle. Krytyka Berkley'a była błędna w tym przypadku: istnieje taka hierarchia. Nasze podstawowe założenie o liczbach hiperrzeczywistych to to, że zawierają przynajmniej jedną nieskończoną liczbę, H, która jest większa od wszystkich liczb całkowitych. Jeśli to jest prawdziwe, to 1/H musi być mniej niż 1/2, mniej niż 1/100, mniej niż 1/1000000 - mniej niż 1/n, dla każdego całkowitego n. Dlatego hiperrzeczywiste gwarantują to, że zawierają również nieskończenie małe liczby więc mamy przynajmniej trzy poziomy hierarchii: nieskończone porównywalne do H, skończone i nieskończenie małe porównywalne do 1/H. Jeśli potrafisz to przełknąć, to nie jest dużym skokiem dodanie kilku innych szczebli do tej drabiny, jak na przykład bardzo nieskończenie małe liczby porównywalne z <latex>\frac{1}{H^2}</latex>. Jeśli wygląda to na podejrzane, myśl o twierdzeniach dotyczących liczb hiperrzeczywistych jako o opisach ograniczania procesów zawierających liczby rzeczywiste. Przykładowo, w ciągu liczb <latex>1,1^2 = 1,21, 1,01^2 = 1,0201, 1,001^2 = 1,002001, …,</latex> jasnym jest, ze liczba reprezentowana prze cyfrę 1 w na końcu rozwinięcia dziesiętnego zmniejsza się szybciej niż wartość dodana (? contribution) z powodu cyfry 2 w środku.

Jedna subtelną kwestią tutaj, o czym wcześniej nie wspomniałem podczas różniczkowania funkcji sinus, jest to, że czy zasada przeniesienia jest wystarczająca by pozwolić nam zdefiniować wszystkie funkcje, które pojawiają się jako znajome klawisze w kalkulatorze: <latex>x^2, \sqrt{x}, \sin{x}, \cos{x}, e^x,</latex> itd. Przecież te funkcje zostały pierwotnie zdefiniowane jako reguły, które pobierały liczbę rzeczywistą jako wejście i podawały na wyjściu również liczbę rzeczywistą. Nie jest oczywistym, że ich definicje można naturalnie rozszerzyć o liczby hiperrzeczywiste i wprowadzać je na wejściu, otrzymywać je na wyjściu. W gruncie rzeczy odpowiedź jest taka, że możemy zastosować zasadę przeniesienia dla nich tak jakbyśmy to zrobili twierdzeniom o prostej arytmetyce.

Kiedy uczyłem się rachunku, wydawało mi się, że skoro pochodna od 3t wynosi 3 a od 7t, 7 to pochodna od t pomnożonego przez t powinna wynosić t a nie 2t. Powodem istnienia czynnika 2 w prawidłowej odpowiedzi jest to, że <latex>t^2</latex> ma dwa powody do rośnięcia gdy i t rośnie: rośnie, ponieważ pierwszy czynnik t rośnie, ale również dlatego, że rośnie i drugi czynnik. Ogólnie, można znaleźć pochodną iloczynu dwóch funkcji wtedy, gdy znamy pochodne poszczególnych funkcji.

<box 80% | Zasada iloczynu:> Jeśli x i y są funkcjami t, to pochodna ich iloczynu wynosi:

<latex> $ \begin{equation*} \frac{d(xy)}{dt} = \frac{dx}{dt}y + x\frac{dy}{dt} \end{equation*} $ </latex> </box>

Dowód jest łatwy. Podstawiając pod t, nieskończenie małą liczbę dt, zmieniamy iloczyn xy o <latex>(x+dx)(y+dy) - xy = ydx + xdy +dxdy</latex> i dzieląc przez dt otrzymujemy <latex>\frac{dx}{dt}y + x\frac{dy}{dt} + \frac{dxdy}{dt}</latex>, czego standardową częścią jest wynik, którego szukamy.

++++ Przykład 12. |

Znajdź pochodną funkcji tsin(t).

<latex> \frac{d(t\sin{t})}{dt} = t\frac{d(\sin{t})}{dt} + \frac{dt}{dt}\sin{t} = t\cos{t} + \sin{t} </latex>

Rysunek 2.5 przedstawia geometryczną interpretację zasady iloczynu. Wyobraźcie sobie króla w jego zamku, w południowo-zachodnim rogu jego królestwa, który wysyła linię piechoty by rozszerzyć swoje królestwo na północ i jazdę konną na wschód. W odstępie czasu dt, jazda konna, która przemieszcza się szybciej, przemierza odległość dx, większą od tej, przemierzonej przez piechotę dy. Jednakże pasek terytorium podbitego przez jazdę, ydx, nie jest tak duży jak mógłby być, ponieważ w naszym przykładzie y nie jest tak duże jak x.

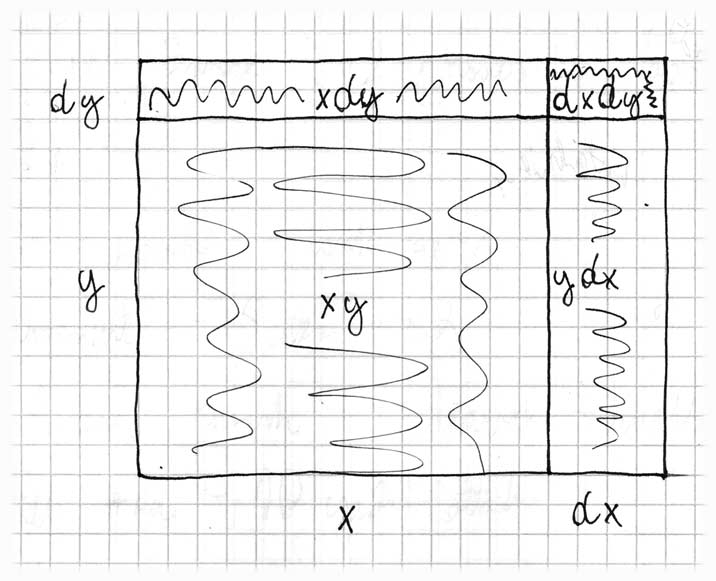
<center><i>Rys. 2.5. Geometryczna interpretacja zasady iloczynu</i></center>
++++

Pomocną zaletą notacji Leibniza jest to, że można łatwo ją wykorzystać, by sprawdzić, czy jednostki rozwiązania mają jakiś sens. Jeżeli mierzymy odległości w metrach a czas w sekundach, to jednostką xy są metry kwadratowe i taką też posiada zmiana pola powierzchni d(xy). Dzieląc przez dt otrzymujemy liczbę metrów kwadratowych przez sekundę bycia podbijanym. Po prawej stronie zasady iloczynu, dx/dt ma jednostkę metrów na sekundę (prędkość) a mnożąc to przez y otrzymujemy metry kwadratowe na sekundę, co jest zgodne z lewą stroną. Jednostki drugiego wyrazu po prawej również się sprawdzają(?). Początkujący mogliby być kuszeni możliwością, że zasada iloczynu wyglądałaby tak d(xy)/dt = (dx/dt)(dy/dt), ale notacja Leibniza pokazuje, że nie można tak zrobić, ponieważ jednostki po lewej, <latex>m^2/s</latex> nie zgadzałyby się z tymi po prawej, <latex>m^2/s^2</latex>.

Ponieważ sprawdzanie jednostek jest tak pomocne, jest specjalna metoda zapisywania drugiej pochodnej w notacji Leibniza. To co Newton zapisywał jako <latex>\ddot{x}</latex>, u Leibniza wyglądało tak: <latex>\frac{d^2x}{dt^2}</latex>. Pomimo innego usytuowania dwójek na górze i dole ułamka może wydawać się niespójne dla wielu początkujących, działa to całkiem nieźle. Jeśli x to odległość mierzona w metrach a t to czas, w sekundach, to druga pochodna powinna mieć jednostkę przyspieszenia, tj. <latex>(m/s)/s,\quad m/s^2</latex>. Notacja Leibniza ma znaczyć dokładnie to: góra ułamka wygląda jakby miała jednostkę metra, ponieważ nie podnosimy x do kwadratu, na dole ułamka mamy sekundy do kwadratu, ponieważ podnosimy dt do kwadratu. Dlatego jednostki są poprawne. Ważne jest, by zdać sobie sprawę z tego, że symbol d to nie liczba (nie rzeczywista ale również nie hiperrzeczywista), więc nie możemy tak naprawdę podnieść go do kwadratu; notacja nie powinna być odbierana dosłownie w przypadku nieskończenie małych wartości.

++++ Przykład 13. |

Ciekawym zastosowaniem zasady iloczynu jest znalezienie pochodnej <latex>\sqrt{t}</latex>. Ponieważ <latex>\sqrt{t}</latex> można zapisać jako <latex>t^{\frac{1}{2}</latex>, możemy podejrzewać, że zasada <latex>d(t^k)/dt = kt^{k-1}</latex> będzie obowiązywać i tutaj więc otrzymamy <latex>\frac{1}{2}t^{\frac{-1}{2} = 1/(2\sqrt{t}</latex>. Jednakże metody wykorzystane do udowodnienia takiej reguły w rozdziale 1 tylko działają dla k będącego liczbą całkowitą, więc najlepszym, co możemy zrobić to potwierdzić nasze przypuszczenie w przybliżeniu graficznie.

Wykorzystując zasadę iloczynu, możemy zapisać <latex>f(t) = d\sqrt{t}/dt</latex> dla naszej nieznanej pochodnej i z powrotem podstawić do wyniku (?) wykorzystując zasadę iloczynu:

<latex> \frac{dt}{dt} = \frac{d(\sqrt{t}\sqrt{t}}{dt} = f(t)\sqrt{t} + \sqrt{t}f(t) = 2f(t)\sqrt{t}</latex>

Ale dt/dt = 1, więc <latex>f(t) = 1/(2\sqrt{t})</latex>, tak jak powinno. ++++

Sztuczka wykorzystana w przykładzie 13 może być wykorzystana by dowieść, że zasada potęgi <latex>d(x^n)/dx = nx^{n-1}</latex> działa w przypadkach, gdzie n jest liczbą całkowitą mniejszą od 0.

• http://pl.wikipedia.org/wiki/Wz%C3%B3r_Leibniza

Rysunek 2.6 pokazuje trzech ludzi na huśtawkach. Ten po lewej stronie przemieszcza się w dól o dx, środkowy podnosi się o dy, co jednocześnie spowoduje ruch tego po prawej w dół o dz. Jeżeli chcemy przewidzieć, jak bardzo ten po prawej przesunie się w odpowiedzi na pewną ilość ruchu tego po lewej, mamy:

<latex> $ \begin{equation*} \frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx} \end{equation*} $ </latex>

Ten związek, zwany regułą łańcuchową, pozwala nam obliczyć pochodną funkcji zdefiniowanej przez funkcję w innej funkcji. Dowód to głównie zastosowanie zasady przenoszenia (jak to często bywa, dowód z wykorzystaniem hiperrzeczywistych jest dużo prostszy).

++++ Przykład 14. | Znajdź pochodną funkcji <latex>z(x) = \sin{(x^2)}</latex>.

Niech <latex>y(x) = x^2</latex>, tak że z(x) = sin(y(x)). Wtedy:

<latex> $ \begin{equation*} \frac{dz}{dx} &= \frac{dz}{dy}\frac{dy}{dx}

            &= \cos{(y)}2x
            &= 2x\cos{(x^2)}

\end{equation*} $ </latex>

Najczęściej mówi się, że reguła łańcuchowa mówi by wziąć pochodną funkcji zewnętrznej, sinusa w tym przypadku, i pomnożyć ją przez pochodną tego co jest wewnątrz, co w naszym przypadku jest kwadratem. Gdy przyzwyczaisz się do tego, nie będziesz musiał wymyślać trzeciej, pośredniej zmiennej, jak zrobiliśmy tutaj z y. ++++

++++ Przykład 15. | Wyraźmy regułę łańcuchową bez użycia notacji Leibniza. Niech funkcja f będzie zdefiniowana przez f(x) = g(h(x)). Wtedy pochodna f wynosi: <latex>f'(x) = g'(h(x))*h'(x)</latex> ++++

Funkcja eksponencjalna

Funkcja eksponencjalna <latex>e^x</latex>, gdzie e = 2,71828… jest podstawą logarytmu naturalnego, pojawia się często w zastosowaniach tak obszernych jak rośnięcie populacji zwierząt czy układach elektrycznych. Jej pochodną otrzymamy przez:

[rysunek 2.6 z trzema ludzikami]

<latex> $ \begin{align*} \frac{de^x}{dx} & = \frac{e^{x+dx} - e^x}{dx}

              & = \frac{e^x e^{dx} - e^x}{dx}\\
              & = e^x\frac{e^{dx} - 1}{dx}

\end{align*} $ </latex>

Drugi czynnik, <latex>e^{dx}-1/dx</latex> nie posiada w sobie x, więc jest to tylko stała. Dlatego wiemy, że pochodną <latex>e^x</latex> jest po prostu <latex>e^x</latex> pomnożone przez jakąś nieznaną stałą, <latex>\frac{de^x}{dx} = ce^x</latex>

Szybkie sprawdzenie tego na wykresie, dla x = 0, pokazuje, że nachylenie jest bliskie 1, więc c jest bliskie 1. Obliczenia numeryczne również pokazują, że na przykład (<latex>e^{0,001} -1)/0,001 = 1,00050016670838</latex> jest bardzo bliskie do 1. Ale skąd wiemy, że jest to dokładnie jeden, gdy dx jest nieskończenie małe? (dowód na stronie 135:/)

++++ Przykład 16 |

Koncentracja pewnej zagranicznej substancji we krwi najczęściej spada eksponencjalnie z czasem: <latex>c = c_{0}e^{-t/a}</latex>, gdzie c₀ to pierwotna koncentracja a a to stała. Dla kofeiny w przypadku dorosłych, a najczęściej wynosi 7 godzin. Przypadek został pokazany na rysunku 2.7. Zróżniczkuj koncentrację z uwzględnieniem czasu i zinterpretuj wynik. Sprawdź jednostki wyniku.

Wykorzystując regułę łańcuchową:

<latex> $ \begin{align*} \frac{dc}{dt} & = c_{0}e^{-t/a}(-\frac{1}{a})

            & = -\frac{c_{0}}{a}e^{-t/a}

\end{align*} $ </latex>

<br> To można zinterpretować jako szybkość, z jaką kofeina jest usuwana z krwi. Jest ujemna, ponieważ koncentracja maleje. Według pierwotnego wyrażenia na x, substancja z dużym a będzie potrzebowała dużo czasu by zmniejszyć swoje stężenie, ponieważ t/a będzie duże tylko wtedy, gdy będziemy mieć duże t, by skompensować duże wartości a. Innymi słowy, większe wartości a oznaczają substancje, których trudniej się pozbyć. Pochodna ma a na dole i interpretacją tego jest to, że dla narkotyku, którego trudno się pozbyć z organizmu, szybkość z którą jest on usuwany z krwi jest mała.

a ma jednostkę czasu, ponieważ funkcja eksponencjalna musi mieć na wejściu (?) liczbę bez jednostki, aby jednostka t/a się skróciła. Jednostka wyniku pochodzi z czynnika c₀/a, i to ma sens, że jednostka to koncentracja podzielona przez czas, ponieważ wynik przedstawia szybkość, z którą koncentracja się zmienia.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -0.50000 : 24.00000 ] noreverse nowriteback set yrange [ -0.50000 : 2.00000 ] noreverse nowriteback set zeroaxis

plot 2*exp(-x/7) </plot> <center><i>Rys. 2.7. Typowy wykres koncentracji kofeiny we krwi, w miligramach na litr, jako funkcja czasu, w godzinach</i></center>
++++

++++ Przykład 17. | Znajdź pochodną funkcji <latex>y = 10^x</latex>.

Ogólnie, jedną z metod radzenia sobie z funkcjami, to przepisanie ich w taki sposób, by otrzymać czynniki, z którymi umiemy sobie poradzić. Powyższa może zostać zapisana jako:

<latex> $ \begin{align*} y & = 10^x
\ln{y} & = \ln{(10^x)}
\ln{y} & = x\ln{10}
y & = e^{x\ln{10}} \end{align*} $ </latex>

Stosując tu regułę łańcuchową, mamy tu pochodną funkcji eksponencjalnej, która jest tą samą funkcją eksponencjalną, pomnożoną przez pochodną tego co wewnątrz:

<latex> \frac{dy}{dx} = e^{x\ln{10}}\ln{10} </latex>

Innymi słowy, “c” o którym mówiliśmy podczas dyskusji o pochodnej <latex>e^x</latex> staje się c = ln10. ++++

Logarytm

Logarytm naturalny to funkcja odwrotna do eksponencjalnej. Mamy więc:

<latex> $ \begin{equation*} \frac{dy}{dx} = \frac{1}{dx/dy} \end{equation*} $ </latex>

gdzie po lewej myślimy o y jako funkcji x, a po prawej uważamy x jako funkcję y. Stosując to do logarytmu naturalnego otrzymujemy:

<latex> $ \begin{align*} y & = \ln{x}
x & = e^y
\frac{dx}{dy} & = e^y
\frac{dy}{dx} & = \frac{1}{e^y}
& = \frac{1}{x}
\frac{d\ln{x}}{dx} & = \frac{1}{x} \end{align*} $ </latex>

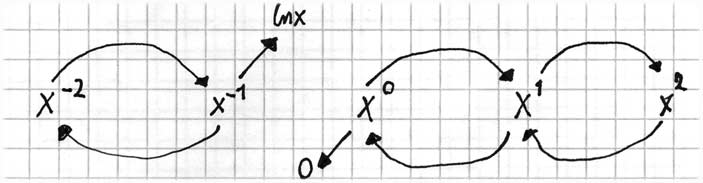
To jest ważne, ponieważ pokazuje, że musi być wyjątek do reguły, że pochodna <latex>x^n</latex> to <latex>nx^{n-1}</latex>, a całka <latex>x^{n-1}</latex> to <latex>x^n/n</latex>.

<center><i>Rys. 2.7. Różniczkowanie i całkowanie funkcji x^n, z pominięciem stałych</i></center>

Całka z <latex>x^-1</latex> nie równa się <latex>x^0/0</latex>, co w ogóle nie miałoby sensu, ponieważ zawiera dzielenie przez zero. Podobnie pochodna od <latex>x^0 = 1</latex> wynosi <latex>0x^{-1}</latex> co równa się zeru. Rysunek 2.7 przedstawia ten pomysł. Funkcje <latex> x^n</latex> formują pewnego rodzaju drabinkę, gdzie różniczkowanie sprowadza nas o szczebelek niżej a całkowanie wyżej. Jednakże istnieją dwa specjalne przypadki, kiedy różniczkowanie zabiera nas w ogóle z drabiny.

++++ Przykład 18. | Dowiedź, że <latex>d(x^n)/dx = nx^{n-1}</latex> dla każdej rzeczywistej wartości n, nie tylko całkowitej.
<latex> $ \begin{align*} y & = x^n
& = e^{n\ln{x}} \end{align*} $ </latex>

Wykorzystując regułę łańcuchową:

<latex> $ \begin{align*} \frac{dy}{dx} & = e^{n\ln{x}}\frac{n}{x}
& = x^n\frac{n}{x}
& = nx^{n-1} \end{align*} $ </latex>

(Dla n = 0, wyniki wynosi 0) ++++

Na początku rozdziału napisaliśmy, że y = lnx. To oznaczało, że ukrycie zakładałem x jako dodatnie. Ogólnie pochodna od ln|x| wynosi 1/x, niezależnie od znaku.

Dotychczas nasze podejście do różniczkowania było pomyślne: reguła iloczynu i reguła łańcuchowa oferują metody rozerwania funkcji na prostsze części a pochodną całości znajdujemy na podstawie wiedzy o pochodnych poszczególnych części. Wiemy, jak znaleźć pochodne sum, różnic i iloczynów, więc oczywistym następnym krokiem jest dzielenie. Jest to jasne, ponieważ wiemy, że pochodna funkcji <latex>1/u = u^{-1}\quad to\quad -u^{-2}</latex>. Niech u i v będą funkcjami x. Wtedy, reguła iloczynu:

<latex> $ \begin{equation*} \frac{d(v/u)}{dx} = \frac{dv}{dx}\frac{1}{u} + v\frac{d(1/u)}{dx} \end{equation*} $ </latex>

i reguła łańcuchowa:

<latex> $ \begin{equation*} \frac{d(v/u)}{dx} = \frac{dv}{dx}\frac{1}{u} - v\frac{1}{u^2}\frac{du}{dx} \end{equation*} $ </latex>

To jest tak proste w wyprowadzeniu, że nie ma sensu uczyć się tego na pamięć. Zauważcie jednak, jak notacja staje się odrobinę dziwaczna, kiedy chcemy zapisać pochodną jak d(v/u)/dx. Kiedy różniczkujemy skomplikowaną funkcję, może być niewygodne wrzucanie wszystkiego do ułamka d../d.. . Czasem lepiej jest zapisać wyrażenie w postaci:

<latex> $ \begin{equation*} \frac{d}{dx}(\frac{v}{u}) \end{equation*} $ </latex>

To może wyglądać jak nadużycie notacji, powodując że d wygląda jak liczba dzielona przez dx. Z drugiej strony, możemy uważać symbol d/dx jako reprezentację różniczkowania po x. Wykorzystując nową notację, reguła współczynników wygląda tak:

<latex> $ \begin{equation*} \frac{d}{dx}(\frac{v}{u}) = \frac{1}{u}\frac{dv}{dx} - \frac{v}{u^2}\frac{du}{dx} \end{equation*} $ </latex>

Znaczenie znaku minusa jest takie, że jeśli u rośnie, v/u maleje.

++++ Przykład 19. | Zróżniczkuj y = x/(1 + 3x), sprawdź, czy wyniki mają jakikolwiek sens.

Identyfikujemy v w x a u w 1 + x. Wynikiem jest:

<latex> $ \begin{align*} \frac{d}{dx}(\frac{v}{u}) & = \frac{1}{u}\frac{dv}{dx} - \frac{v}{u^2}\frac{du}{dx}
& = \frac{1}{1+3x} - \frac{3x}{(1 + 3x)^2} \end{align*} $ </latex>

Jednym sposobem na sprawdzenie wyników jest sprawdzenie ekstremalnych wartości x. Dla bardzo dużych wartości x, 1 na dole x/(1+3x) staje się nieistotna w porównaniu do 3x, a funkcja y dąży do x/3x = 1/3, jej limitu. Dlatego spodziewamy się, że pochodna dy/dx dąży do zera, ponieważ pochodna stałej jest równa zero. I to działa: podstawiając coraz większe wartości pod x dla pochodnej generuje coraz mniejsze wyniki. (W drugim składniku, mianownik zwiększa się szybciej niż licznik, ponieważ ma w sobie kwadrat).

Drugim sposobem jest sprawdzenie jednostek. Załóżmy, w dowolny sposób (arbitrarily), że x ma jednostkę litra (jeśli trójka na dole jest bez jednostki, to jedynka musiałaby reprezentować 1 litr, ponieważ nie można dodawać rzeczy o różnych jednostkach). Funkcja y jest zdefiniowana przez wyrażenie o jednostce litrów podzielonych przez litry, więc y jest bez jednostki. Dlatego pochodna dy/dx powinna mieć jednostkę odwrotności litra. Oba składniki wyrażenia na pochodną posiadają te jednostki, więc wynik jest poprawny. ++++

Intuicyjnie ciągła funkcja to taka funkcja, której wykres nie ma nagłych skoków; cały wykres jest w jednym, połączonym kawałku. Formalnie, funkcja f(x) jest zdefiniowana jako ciągła, gdy dla każdej rzeczywistej i dla każdej nieskończenie małej dx, f(x + dx) - f(x) jest nieskończenie małe.

++++ Przykład 26. | Niech funkcja f będzie zdefiniowana przez f(x) = 0 dla <latex>x\leqslant 0</latex> i f(x) = 1, dla x > 0. Wtedy f(x) jest nieciągła, ponieważ dla dx > 0, f(0 + dx) - f(0) = 1, co nie jest nieskończenie małe.

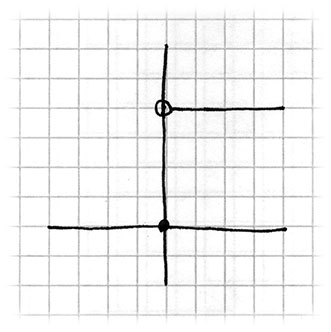
<center><i>Rys. 2.8. Czarna kropka mówi nam, że dolny promień jest częścią promienia, a biała kropka to odwrotność czarnej kropki dla promienia na górze</i></center>
++++

Jeśli funkcja jest nieciągła w danym punkcie, nie jest w tym punkcie różniczkowalna. Z drugiej strony, przykładowe y = |x| pokazuje, że funkcja może być ciągła ale nieróżniczkowalna.

W większości wypadków nie ma powodu by przywoływać definicję tylko po to by sprawdzić (? explicitly), czy dana funkcja jest ciągła. Większość funkcji, z którymi pracujemy, są definiowane z prostszych funkcji, jak z klocków. Przykładowo, załóżmy że już sprawdziliśmy ciągłość funkcji g(x) = 3x i h(x) = sin(x). Później gdybyśmy mieli do czynienia z funkcją f(x) = sin(3x), możemy od razu powiedzieć, że jest ciągła, ponieważ funkcja f(x) = h(g(x)). Taka metoda łączenia funkcji nazywa się złożeniem funkcji. Złożenie dwóch ciągłych funkcji jest również ciągłe. Należy uważać przy dzieleniu: funkcja f(x) = 1/x jest ciągła wszędzie za wyjątkiem x = 0, więc przykładowo 1/sin(x) jest ciągła wszędzie z wyłączeniem wielokrotności <latex>\pi</latex>, gdzie sinus osiąga zero.

Twierdzenie Darboux

Inaczej spojrzenie na ciągłość funkcji umożliwia twierdzenie Darboux. Intuicyjnie, mówi, że jeśli ciągle przemieszczasz się wzdłuż drogi od punktu A do B, musisz minąć wszystkie inne punkty leżące wzdłuż drogi. Bardziej formalnie, twierdzenie mówi, że jeśli y jest ciągłą funkcją, przyjmującą wartości rzeczywiste, w przedziale od a do b (w rzeczywistych ? odstępach) i jeżeli y przyjmuje wartości y₁ i y₂ w pewnych punktach w tym przedziale, to dla każdego y₃ pomiędzy y₁ a y₂ jest pewne rzeczywiste x w przedziale, dla którego y(x) = y₃.

<center><i>Rys. 2.9. Twierdzenie Darboux mówi, że jeśli funkcja jest ciągła, musi przejść przez y3</i></center>

Twierdzenie Darboux wydaje się tak interesujące, że gdybyśmy chcieli zabrać się do jego udowodnienia moglibyśmy czuć się tak jakbyśmy mieli udowodnić propozycję (?) taką jak to “ czy istnieje liczbą większa od 10”. Jeśli kolega chciałby się z tobą założyć o sześciopak, że nie mógłbyś udowodnić tego za pomocą całej (?) matematyki, musiałbyś zmusić kolegę do tego, by dokładnie sprecyzował, z którymi faktami dotyczącymi liczb całkowitych możesz zacząć jako z początkowymi założeniami. Czy wolno ci założyć, że 1 istnieje? Czy uwierzy ci, że skoro istnieje liczba n, to istnieje również liczba n + 1? Twierdzenie Darboux jest bardzo podobne. Jest uznawane, jako twierdzenie o pewnych typach funkcji, ale jego prawda to nie sprawa właściwości funkcji, ale bardziej właściwości danego systemu liczb.

++++ Przykład 27. | Wykaż, że istnieje rozwiązanie równania <latex>10^x + x = 1000</latex>.

Spodziewamy się rozwiązania w pobliżu x = 3, gdzie funkcja <latex>10^x + x = 1003</latex> jest tylko trochę za duża. Z drugiej strony, f(2) = 102 jest dużo za mała. Ponieważ f przyjmuje wartości mniejsze i większe od 1000 w przedziale od 2 do 3 i f jest ciągła, twierdzenie Darboux dowodzi, że istnieje rozwiązanie pomiędzy 2 i 3. Jeżeli chcielibyśmy znaleźć lepsze przybliżenie rozwiązania, moglibyśmy tego dokonać za pomocą metody Newtona wprowadzonej w rozdziale 4.1. ++++

++++ Przykład 28. | Wykaż, że istnieje przynajmniej jedno rozwiązanie równania cos x = x i podaj granice (ramy) jego miejsca.

To jest przestępne równanie i żadne przekształcenia algebraiczne czy trygonometryczne nie dadzą nam rozwiązania, które będzie można zapisać skończoną liczbą arytmetycznych operacji by dać dokładny wynik. Jednakże, łatwo możemy dowieść, e przynajmniej jedno rozwiązanie istnieje, stosując twierdzenie Darboux do funkcji x - cosx. Funkcja cosinus jest ograniczona przez -1 i 1, więc musi być ujemna dla x < -1 i dodatnia dla x > 1. Za twierdzeniem Darboux, musi być rozwiązanie w przedziale <latex>-1\leqslant x\leqslant 1</latex>. Wykres na rysunku 2.10 potwierdza to i pokazuje, że istnieje tylko jedno rozwiązanie.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -8.00000 : 8.00000 ] noreverse nowriteback set yrange [ -8.00000 : 8.00000 ] noreverse nowriteback set zeroaxis

plot x - cos(x) </plot> <center><i>Rys. 2.10. Funkcja x - cosx z przykładu 28</i></center>
++++

++++ Przykład 29. | Dowiedź, że każdy nieparzysty rząd wielomianu P z rzeczywistymi współczynnikami ma przynajmniej jeden rzeczywisty pierwiastek x (punkt, w którym P(x) = 0).

Przykład 28 mógł wywołać wrażenie, że nie ma nic, czego można by się dowiedzieć z twierdzenia Darboux, czego nie moglibyśmy dostrzec na wykresie, ale tego przykładu nie da się rozwiązać wykresem, ponieważ chcemy dowieść ogólny wynik dla wszystkich wielomianów. By zobaczyć, że ograniczenie do rzędów nieparzystych jest konieczne, rozważ wielomian <latex>x^2+1</latex>, które nie posiada żadnych rzeczywistych pierwiastków, ponieważ <latex>x^2 > 0</latex> dla każdej rzeczywistej liczby x.

Aby nie pracować na abstrakcyjnych równaniach, przyjmijmy następujący przykład wielomianu: <latex>P(x) = x^3 - x + 17</latex>. Dla dużych wartości x, liniowe i stałe wyrazy (składniki) będą pomijalne w porównaniu do składnika <latex>x^3</latex>, a ponieważ <latex>x^3</latex> jest dodatni dla dużych wartości x a ujemny dla dużych ujemnych wartości, wnioskujemy że P jest czasem dodatni a czasem ujemny.

Generalizując, przypuśćmy, ze mieliśmy wielomian nieparzystego rzędu n, który zawsze miał ten sam znak dla każdego rzeczywistego x. Wtedy, poprzez zasadę przenoszenia (transfer principle), to samo byłoby prawdziwe dla hiperrzeczywistej wartości x. Jeżeli więc x jest nieskończone, wtedy składowe niższych rzędów są nieskończenie małe w porównaniu do wyrazu <latex>x^n</latex>, a znak wyniku jest określany tylko przez składnik <latex>x^n</latex>, ale <latex>x^n</latex> i <latex>(-x)^n</latex> mają przeciwne znaki i dlatego P(x) i P(-x) mają przeciwne znaki. To jest sprzeczność, więc odkryliśmy założenie, że P zawsze miało ten sam znak dla rzeczywistego x. Ponieważ P jest czasem dodatnie a czasem ujemne, możemy wywnioskować za pomocą twierdzenia Darboux, że gdzieś P jest równe zeru. ++++

++++ Przykład 30. | Dowiedź, że równanie x = sin 1/x ma nieskończenie wiele rozwiązań.

To kolejny, nierozwiązywalny za pomocą wykresu, przykład; patrząc na wykres na rysunku 2.11 nie ma sposobu, żeby dowieść, że przechodzi przez oś x nieskończenie wiele razy. Wykres pomaga nam jednak zobaczyć, co się tam właściwie dzieje. Gdy x maleje, 1/x idzie w górę a sin(1/x) oscyluje szybciej i szybciej. Funkcja nie jest zdefiniowana w 0, ale jest ciągła wszędzie poza zerem, więc możemy zastosować twierdzenie Darbouxa dla każdego przedziału nie zawierającego 0.

Chcemy dowieść, że dla każdego dodatniego u, istnieje takie x, że 0 < x < u, dla którego f(x) ma którykolwiek z pożądanych znaków. Przypuśćmy, że to nie jest prawda dla jakiegoś rzeczywistego u. Wtedy, za pomocą zasady przenoszenia (transfer rule) nieistnienie jakiegokolwiek rzeczywistego x z pożądanymi właściwościami implikuje nieistnienie takiego hiperrzeczywistego x. Ale dla nieskończenie małego x, znak f jest określany całkowicie przez współczynnik przy sinusie, gdyż ten współczynnik jest skończony a współczynnik liniowy nieskończenie mały. Oczywiście sin (1/x) nie może mieć tego samego znaku dla każdej wartości x mniejszej od u, więc jest to sprzeczność a twierdzenie jest poprawne dla każdego u. Z twierdzenia Darbouxa wynika, że istnieje nieskończenie wiele rozwiązań równania.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -2.00000 : 2.00000 ] noreverse nowriteback set yrange [ -2.00000 : 2.00000 ] noreverse nowriteback set zeroaxis

plot x - sin(1/x) </plot> <center><i>Rys. 2.11. Funkcja x - sin(1/x)</i></center>

++++

Extreme Value Theorem

W rozdziale pierwszym widzieliśmy, że znajdywanie maksim i minim funkcji może być trudne, gdyż jest wiele różnych możliwości, w jakie funkcja osiągnie ekstremum: na przykład w punkcie końcowym, w miejscu gdzie jej pochodna wynosi zero lub w nieróżniczkowalnym zgięciu (kink). Extreme Value Theorem umożliwia nam formułowanie bardzo ogólnych twierdzeń o wszystkich tych możliwościach, zakładając tylko ciągłość badanej funkcji.

Extreme Value Theorem mówi, że jeśli f to ciągła funkcja o wartościach rzeczywistych w rzeczywistym przedziale definiowanym przez <latex>a\leqslant x\leqslant b</latex> to f ma maksymalne i minimalne wartości w tym przedziale, które są osiągane w specyficznych punktach przedziału.

Zobaczmy najpierw dlaczego te założenia są konieczne. Jeśli nie bylibyśmy związani ze skończonym przedziałem, to y = x mogłoby być kontrprzykładem, ponieważ jest ciągły i nie przyjmuje żadnych minimalnych i maksymalnych wartości. Jeżeli nie założylibyśmy, że funkcja jest ciągła, wtedy moglibyśmy zdefiniować ją jako y = x dla x < 1 i y = 0 dla <latex>x \geqslant 1</latex>; ta funkcja nigdy nie jest większa od 1, ale nigdy nie osiąga 1 dla żadnej konkretnej wartości x.

++++ Przykład 31. | Znajdź maksymalną wartość wielomianu <latex>P(x) = x^3 + x^2 +x +1</latex> dla <latex>-5 \leqslant x\leqslant 5</latex>.

Wielomiany są ciągłe, więc extreme value theroem gwarantuje istnienie takich maksimów. Załóżmy, że próbujemy je znaleźć w miejscu, gdzie jego pochodna wynosi zero. Pochodna wielomianu to <latex>3x^2 + 2x + 1</latex> a przyrównując ją do zera daje równanie kwadratowe ale podanie kwadratowego wzoru pokazuje, że nie ma rzeczywistych rozwiązań. Wygląda na to, że funkcja nie ma nigdzie maksimum (nawet poza naszym przedziałem), które wyglądałoby jak płynny szczyt. Ponieważ nie posiada żadnych nieciągłości czy zgięć, jest tylko jeden typ maksimum, który mogłaby posiadać, czyli maksimum na którymś z jej końców. Wstawiając granice, widzimy że P(-5) = -104 a P(5) = 156, więc największa wartość w tym przedziale to 156 ++++

Historycznie, rachunek różniczkowo-całkowy nieskończenie małych, taki jak stworzony przez Newtona i Leibniza, został przeinterpretowany w XIX wieku przez Cauchy'ego, Bolzano i Weierstrassa dla granic (in terms of limits). Wszyscy matematycy nauczyli się obu języków i swobodnie przełączali się między nimi. Ci, którzy uczyli się w nieskończenie małych, gdy usłyszą twierdzenie z wykorzystaniem języka granic, przetłumaczą je sobie w nieskończenie małe; dla nich, każde twierdzenie o granicach było naprawdę o nieskończenie małych. Dla ich młodszych kolegów, nauczonych z wykorzystaniem granic, każde twierdzenie o nieskończenie małych miało być rozumiane jako skrót (? shorthand) dla metody granic. Gdy Robinson w latach sześćdziesiątych opracował podstawy hiperrzeczywistego systemu liczb, częstym zarzutem było to, że to właściwie nic nowego, ponieważ każde twierdzenie o nieskończenie małych było po prostu inaczej przedstawionym twierdzeniem o granicach; oczywiście to samo można powiedzieć o pracy Weierstrassa z poprzedniego wieku! W rzeczywistości, wszyscy praktycy rachunku zdali sobie sprawę z tego, że różne podejścia do tematu lepiej działały z różnymi problemami. Definicja granicy według Weierstrassa brzmi:

<box 80% | Definicja granicy:> Mówimy, że l jest granicą funkcji f(x) gdy x dąży do a, tj.

<latex> $ \begin{equation*} \lim_{x\rightarrow a} f(x) = \ell \end{equation*} $ </latex>

jeśli następujące jest prawdziwe: dla każdej rzeczywistej liczby <latex>\epsilon</latex> istnieje inna rzeczywista liczba <latex>\delta</latex>, taka że dla wszystkich x z przedziału <latex>a-\delta\le x \le a+\delta</latex>, wartość f jest w zakresie od <latex>\ell-\epsilon$ to $\ell+\epsilon</latex> </box>

Intuicyjnie, idea jest taka, że jeśli chcę abyś zrobił f(x) bliskie l, muszę tylko ci powiedzieć jak blisko a ty możesz mi powiedzieć, że będzie tak blisko dopóki x jest w pewnej odległości od a.

W przypadku nieskończenie małych mamy:

<box 80% | Definicja granicy:> Mówimy, że l to granica funkcji f(x) gdy x dąży do a, tj.

<latex> $ \begin{equation*} \lim_{x\rightarrow a} f(x) = \ell \end{equation*} $ </latex>

jeśli następujące jest prawdziwe: dla każdej nieskończenie małej liczby dx, wartość f(a + dx) jest skończona, a podstawowa część f(a + dx) równa sie l. </box>

Obydwie definicje są równoważne. Czasem granica może zostać określona po prostu przez podstawienie liczb:

++++ Przykład 32. | Określ:

<latex> $ \begin{equation*} \lim_{x\to 0}\frac{1}{1+x} \end{equation*} $ </latex>


Podstawiamy x = 0 i widzimy, że granica wynosi 1. ++++

W niektórych przykładach, podstawianie nie skutkuje, jeżeli zrobimy to bezpośrednio, ale będzie możliwe, jeżeli przekształcimy wyrażenie:

++++ Przykład 33. | Określ:

<latex> $ \begin{equation*} \lim_{x\to 0}\frac{\frac{2}{x}+7}{\frac{1}{x}+8686} \end{equation*} $ </latex>


Podstawianie x = 0 nie daje wyniku, ponieważ nie dzielimy przez zero.

Intuicyjnie spodziewamy się, że granica będzie dobrze zdefiniowana i będzie wynosić 2, ponieważ dla bardzo małych wartości x, licznik będzie zdominowany przez wyraz 2/x a mianownik przez wyraz 1/x, więc wyrazy 7 i 8686 będą liczyły się mniej i mniej gdy x będzie malało.

By przedstawić to bardziej drobiazgowo, możemy pomnożyć licznik i mianownik ułamka przez x otrzymując:

<latex> $ \begin{equation*} \frac{2+7x}{1+8686x} \end{equation*} $ </latex>

co z kolei równa się 2, jeżeli podstawimy pod x = 0, więc granica wynosi 0.

Ten przykład jest troszkę delikatny, ponieważ gdy x = 0, funkcja jest nieokreślona a ponadto nie byłoby poprawne mnożyć górę i dół ułamka przez x. Ogólnie nie jest algebraicznie poprawnie mnożyć górę i duł ułamka przez 0, ponieważ wynikiem jest 0/0, co jest nieokreślone. Ale my właściwie nie pomnożyliśmy przez 0, ponieważ nigdy nie pozwalamy x osiągnąć 0. Obie definicje odnoszą się do funkcji w obszarze bardzo bliskim punktowi granicznemu, a nie w punkcie granicznym.

Jest to przykład, w którym funkcja nie była dobrze określona w pewnym punkcie a mimo tego granica funkcji była określona dobrze, gdy się do tego punktu zbliżaliśmy. W przypadku takim jak ten, gdzie tylko jednego punktu brakuje w dziedzinie funkcji, naturalnym jest rozszerzenie definicji funkcji poprzez wypełnienie tej dziury. Przykład 35 poniżej pokazuje, że taka metoda nie jest zawsze możliwa. ++++

++++ Przykład 34. |

Zbadaj zachowanie się granicy <latex>1/x^2</latex> gdy x dąży do 0 i 1.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -2.00000 : 2.00000 ] noreverse nowriteback set yrange [ -0.60000 : 4.00000 ] noreverse nowriteback set zeroaxis

plot 1/(x*x) </plot> <center><i>Rys. 2.12. Funkcja 1/x^2 z przykładu 34</i></center>

W x = 1, podstawianie działa i widzimy, że granica wynosi 1.
W x = 0, podstawianie nie działa, gdyż dzielenie przez 0 jest nieokreślone. Stosując definicję granicy wyrażonej przez nieskończenie małe, granica x dąży do 0, musimy więc sprawdzić, czy <latex>1/(0 + dx)^2</latex> jest skończone dla nieskończenie małego dx i, jeśli tak, czy zawsze ma tą samą podstawową część. Ale oczywistym jest, że <latex>1/(0+dx)^2 = dx^{-2}</latex> jest zawsze nieskończone, więc stwierdzamy, że ta granica jest nieokreślona. ++++

++++ Przykład 35. | Zbadaj zachowanie się granicy funkcji <latex>f(x)=\tan^{-1}{(1/x)}</latex> gdy x dąży do 0.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -6.00000 : 6.00000 ] noreverse nowriteback set yrange [ -2.00000 : 2.00000 ] noreverse nowriteback set zeroaxis

plot atan(1/x) </plot> <center><i>Rys. 2.13. Funkcja f(x) z przykładu 35</i></center>

Podstawianie nie działa, ponieważ dzielenie przez zero jest nieokreślone.
Z definicji o granicy nieskończenie małych, pierwszym warunkiem jest to, żeby f(0 + dx) było skończone dla nieskończenie małych wartości dx. Wykres z rysunku 2.13 pokazuje, że jest to prawdopodobne i faktycznie możemy temu dowieść za pomocą zasady przenoszenia (transfer principle). Dla każdego rzeczywistego x mamy <latex>-\pi\leqslant f(x) \leqslant \pi\2</latex>, a przez 'transfer principle' to jest prawdziwe i dla hiperrzeczywitych i dlatego f(0 + dx) jest skończone. Drugim warunkiem jest to, żeby standardowa część f(0 + dx) miała wyjątkową, zdefiniowaną (?) wartość. Wykres pokazuje, że mamy dwa przypadki do rozważenia, jedno po prawej stronie wykresu a druga po lewej. Intuicyjnie spodziewamy się, że standardowa część f(0 + dx) będzie równa <latex>\pi/2</latex> dla dodatniego dx i <latex>-\pi/2</latex> dla ujemnego i dlatego druga część definicji nie będzie spełniona. Dla bardziej formalnego dowodu, możemy wykorzystać 'transfer principle'. Dla rzeczywistego x dla 0 < x < 1, na przykład, f jest zawsze dodatnie i większe od 1, więc na podstawie 'transfer principle' f(0 + dx) > 1 dla dodatniego, nieskończenie małego dx. Ale podobnie, możemy być pewni, że f(0 + dx) < -1, gdy dx jest ujemne i nieskończenie małe. Dlatego standardowa część f(0 + dx) może mieć różne wartości dla różnych, nieskończenie małych wartości dx i stwierdzamy, że granica jest nieokreślona.

W podobnych przypadkach możemy zdefiniować granicę jednostronną, zapisaną tak:

<latex> $ \begin{equation*} \lim_{x\to 0^-}\tan^{-1}\frac{1}{x} = -\frac{\pi}{2} \end{equation*} $ </latex>

<latex> $ \begin{equation*} \lim_{x\to 0^+}\tan^{-1}\frac{1}{x} = \frac{\pi}{2} \end{equation*} $ </latex>
++++

Reguła de l'Hospitala

Rozważmy granicę:

<latex> $ \begin{equation*} \lim_{x\to 0}\frac{\sin{x}}{x} \end{equation*} $ </latex>

Podstawianie nie działa, bo dostajemy 0/0. Dzielenie jest niezdefiniowane, w obu systemach (rzeczywistym i hiperrzeczywistym). Niezerowa liczba podzielona przez małą liczbę daje dużą liczbę; niezorwa liczba podzielona przez bardzo małą liczbę daje bardzo dużą liczbę; niezerowa liczba podzioelona przez nieskończenie małą liczbę daje nieskończoną liczbę. Z drugiej strony, dzielenie zero przez zero oznacza szukanie rozwiązania do równania 0 = 0q, gdzie q jest wynikiem dzielenia. Ale dla każdego q istnieje rozwiązanie tego równania, więc nawet pobieżnie nie jest poprawnym powiedzenie, że 0/0 to nieskończoność; to nie nieskończoność, to cokolwiek, co byśmy chcieli.

Ponieważ podstawianie zera nie działało, spróbujmy za x podstawić liczbę, która jest mała, lecz większa od zera.

<latex> $ \begin{equation*} \frac{\sin{0,00001}}{0,00001} = 0,999999999983333 \end{equation*} $ </latex>

Wygląda na to, że granica jest równa 1. To jest idea definicji granicy Weierstrassa: wydaje się, że możemy otrzymać odpowiedź tak bliską do 1 jaką byśmy chcieli, jeżeli jesteśmy skłonni zrobić x tak bliskie 0 jak to potrzebne. Wykres na rysunku 2.14 to ilustruje.

<plot> unset border set xtics axis nomirror set ytics axis nomirror set zeroaxis set xrange [ -20.00000 : 20.00000 ] noreverse nowriteback set yrange [ -0.50000 : 1.00000 ] noreverse nowriteback set zeroaxis

plot sin(x)/x </plot> <center><i>Rys. 2.14. Wykres funkcji sinx/x</i></center>

Ogólny pomysł jest taki, że dla małych wartości x, przybliżenie dla małego kąta <latex>\sin{x}\approx x</latex> osiąga (obtains??), a gdy x staje się mniejsze i mniejsze, przybliżenie jest coraz dokładniejsze, więc sinx/x zbliża się do 1.

Ale wciaż nie dowiedliśmy, że granica wynosi dokładnie 1. Spróbujmy użyć definicji granicy z nieskończenie małymi.

<latex> $ \begin{align*} \lim_{x\to 0}\frac{\sin{x}}{x} &= \st\left [\frac{\sin{(0 + dx)}}{0+dx}\right]
&= \st\left [\frac{dx + …}{dx}\right] \end{align*} $ </latex>

gdzie … to współczynniki rzędu <latex>dx^2</latex>. Więc

<latex> $ \begin{align*} \lim_{x\to 0}\frac{\sin{x}}{x} &= \st\left [1+\frac{\ldots}{dx}\right]
&= 1 \end{align*} $ </latex>

To specyficzny przypadek następującej zasady do obliczania granic zawierających 0/0:

<box 80% | Reguła de l'Hospitala> Jeśli u i v są funkcjami z u(a) = 0 i v(a) = 0, pochodne <latex>\dot{u}(a)</latex> i <latex>\dot{v}(a)</latex> są określone i pochodna <latex>\dot{v}(a)\neq 0</latex>, to:

<latex> $ \begin{equation*} \lim_{x\to a}\frac{u}{v} = \frac{\dot{u}(a)}{\dot{v}(a)} \end{equation*} $ </latex>
</box>

Dowód: Ponieważ u(a) = 0 i pochodna du/dx jest określona w a, u(a+dx) = du jest nieskończenie małe i również takie jest v. Przez definicję granicy, standardowa część:

<latex> $ \begin{equation*} \frac{u}{v} = \frac{du}{dv} = \frac{du/dx}{dv/dx} \end{equation*} $ </latex>

gdzie, przez założenie, licznik i mianownik są określone ( i skońćzone, ponieważ pochodna jest określona “in terms of the standard part??”). Część standardowa współczynnika takiego jak pq równa się czynnikowi standardowych części, zakładając że p i q są skończone (co już ustaliliśmy), i że <latex>q\neq 0</latex> (co jest prawdziwe z założenia). Ale standardowa część du/dx jest definicją pochodnej <latex>\dot{u}</latex> podobnie jest z dv/dx, więc to ustala wynik.

++++ Przykład 36. | Oszacuj:

<latex> $ \begin{equation*} \lim_{x\to 0}\frac{e^x-1}{x} \end{equation*} $ </latex>

Obliczając pochodne licznika i mianownika ułamka, znajdujemy że <latex>e^x/1</latex>, co równa się 1, gdy obliczane w x = 0. ++++

++++ Przykład 37. | Oszacuj:

<latex> $ \begin{equation*} \lim_{x\to 1}\frac{x-1}{x^2-2x+1} \end{equation*} $ </latex>

Podstawiając x = 1 nie działa, ponieważ góra i dół ułamka równałyby się zeru. Obliczając pochodne góry i dołu mamy 1/(2x - 2), które biegnie w górę gdy x = 1. Aby symbolicznie to zapisać:

<latex> $ \begin{equation*} \lim_{x\to 1}\frac{x-1}{x^2-2x+1}=\infty \end{equation*} $ </latex>
++++

W następnym przykładzie, będziemy musieli wykorzystać regułę de l'Hospitala dwukrotnie, zanim otrzymamy odpowiedź. ++++ Przykład 38. | Oszacuj:

<latex> $ \begin{equation*} \lim_{x\to \pi}\frac{1+\cos{x}{(x-\pi)^2} \end{equation*} $ </latex>

Stosując zasadę de l'Hospitala otrzymujemy:

<latex> $ \begin{equation*} \frac{-\sin{x}}{2(x-\pi)} \end{equation*} $ </latex>

co w dalszym daje 0/0, gdy podstawimy <latex>x = \pi</latex>. Powtarzając poprzedni krok, otrzymujemy:

<latex> $ \begin{equation*} \frac{-\cos{x}}{2} = \frac{1}{2} \end{equation*} $ </latex>
++++

Inne spojrzenie na nieokreślone formy (forms?)

O wyrażeniach podobnych do 0/0, nazywanych formą nieokreśloną, można myśleć inaczej w przypadku wyrazów nieskończenie małych. Przypuśćmy, że mam dwie nieskończenie małe liczby d i e schowane w kieszeni. Pytam cię, czy d/e jest skończone, nieskończony czy nieskończenie małe. Nie możesz odpowiedzieć, ponieważ d i e mogą nie być nieskończenie małymi tego samego rzędu wielkości. Na przykład, jeśli e = 37d, to d/e = 1/37, co jest skończone, ale jeśli <latex>e = d^2</latex>, to d/e jest nieskończone; a jeśli <latex>d = e^2</latex>, to d/e jest nieskończenie małe. Podstawiajc do tego liczby bardzo małe ale nie nieskończenie małe:

<latex> $ \begin{align*} \frac{0,001}{0,037} &= \frac{1}{37}
\frac{0,001}{0,000001} &= 1000
\frac{0,000001}{0,001} &= 0,001 \end{align*} $ </latex>

Z drugiej strony, przypuśćmy, że mówię ci, że mam nieskończenie małą liczbę d i skończoną liczbę x i proszę cię o spekulacje o d/x. Z pewnością wiesz, że będzie to nieskończenie mała liczba. Podobnie można być pewnym, że x/d jest nieskończone. To nie są nieokreślone formy.

Możemy zrobić coś podobnego z nieskończonymi liczbami. Jeśli H i K są nieskończone, to H - K jest nieokreślone. Mogłoby być nieskończone, jeśli na przykład H byłoby dodatnią nieskończonością a K = H/2. Z drugiej strony mogłyby być skończone jeśli H = K + 1. Podstawiając duże, ale skończone liczby:

<latex> $ \begin{align*} 1000 - 500 &= 500
1001 - 1000 &= 1 \end{align*} $ </latex>

++++ Przykład 39. | Jeśli H jest nieskończoną dodatnią liczbą, czy <latex>\sqrt{H+1} - \sqrt{H-1}</latex> jest skończone, nieskończone, nieskończenie małe czy nieokreślone?

Próbując z dużą liczbą skończoną, mamy:

<latex> $ \begin{equation*} \sqrt{1000001} - \sqrt{999999} = 1,000000020373 * 10^{-3} \end{equation*} $ </latex>
co jest liczbą przypominającą nieskończenie małe. Bardziej rygorystycznie możemy zapisać wyrażenie jako <latex>\sqrt{H}(\sqrt{1+\frac{1}{H}} - \sqrt{1-\frac{1}{H}}</latex>. Ponieważ pochodna pierwiastka kwadratowego <latex>\sqrt{x}</latex> w x = 1 wynosi 1/2, możemy to aproksymować jako:

<latex> $ \begin{equation*} \sqrt{H}[1+\frac{1}{2H} + … - (1 - /frac{1}{2H} + … )] = \sqrt{H}[\frac{1/H} + …] = \frac{1}{\sqrt{H}} \end{equation*} $ </latex>

co jest nieskończenie małą. ++++

Granice w nieskończoności

Definicja granicy w przypadku nieskończenie małych “extends” natychmiast do granicy procedur, w których x rośnie a nie zbliża się do skończonej wartości. Na przykład funkcja 3 + 1/x przybliża się do 3 gdy x rośnie. Jeśli a jest liczbą nieskończoną, to definicja mówi, że rozwiązując to równanie w a + dx, gdzie dx jest nieskończenie małe, daje wynik , którego część standardowa (std part) wynosi 3. Nie ma znaczenia fakt, że a jest nieskończone, definicja w dalszym ciągu jest prawdziwa. Zauważyć można również, że w tym przykładzie nie ma znaczenia jaką nieskończoną liczbą jest a; granica wynosi 3 dla jakiejkolwiek nieskończonej a. Możemy to zapisać jako:

<latex> $ \begin{equation*} \lim_{x\to \infty}3+\frac{1}{x} = 3 \end{equation*} $ </latex>

gdzie symbol nieskończoności może być zinterpretowany jako: “taa, taa… nie obchodzi mnie jaką nieskończoną liczbę tu wstawisz, ja utrzymuję, że i tak wyjdzie 3”. Symbol <latex>\infty</latex> nie może być interpretowany jako podstawiany za jakąkolwiek nieskończoną liczbę.

Innym przykładem jest funkcja arctangens. Arctangens 1000 wynosi w przybliżeniu 1,5698 a podstawiając coraz większe liczby daje wyniki zbliżające się do <latex>\pi/2 \approx 1,5707</latex>. Ale arctangens -1000 to w przybliżeniu -1,5698, bardzo blisko <latex>-\pi/2</latex>. Z tych obserwacji wynika, że:

<latex> $ \begin{equation*} \lim_{x\to a}\arctan{x}^{-1} \end{equation*} $ </latex>

wynosi <latex>\pi/2</latex> dla dodatnich nieskończonych a, ale <latex>-\pi/2</latex> dla ujemnych nieskończonych a. Poniższy zapis nie jest poprawny:

<latex> $ \begin{equation*} \lim_{x\to a}\arctan{x}^{-1} = \frac{\pi}{2} \end{equation*} $ </latex>

ponieważ to, jaką liczbę nieskończoną wybierzemy ma znaczenie. Zapisujemy więc raczej:

<latex> $ \begin{equation*} \lim_{x\to +\infty}\arctan{x}^{-1} = \frac{\pi}{2} \lim_{x\to -\infty}\arctan{x}^{-1} = -\frac{\pi}{2} \end{equation*} $ </latex>

Niektóre wyrażenia nie mają takiej granicy w ogóle. Na przykład, jeżeli weźmiemy sinusa dużej liczby (tysiąc, milion) na kalkulatorze, wyniki to właściwie losowe liczby z przedziału od -1 do 1. Nie przyjmują żadnej konkretnej wartości, ponieważ funkcja sinusa oscyluje tam i z powrotem cały czas. Aby formalnie dowieźć, że <latex>\lim_{x\to +\infty}\sin{x}</latex> jest nieokreślone, rozważ że funkcja sinus, określona tylko na liczbach rzeczywistych, ma taką właściwość, że można zmienić jej wynik o przynajmniej 0,1 jeśli doda się 1,5 lub -1,5 do wartości wchodzącej (input). Na przykład <latex>\sin{0,8} \approx 0,717</latex> a <latex>\sin{(0,8-1,5)} \approx -0,644</latex>. Stosując tu regułę przenoszenia, widzimy że to jest również prawdziwe dla liczb hiperrzeczywistych. Dlatego nie może być żadna wartość l, która nieskończenie mało różni się od sina dla wszystkich dodatnich nieskończonych wartości a.

Często interesuje nas znalezienie granicy, gdy x dąży do nieskończoności, wyrażenia które zapisane jest w nieokreślonej formie jak H/K, gdzie H i K są nieskończone.

++++ Przykład 40. | Wyznacz granicę

<latex> $ \begin{equation*} \lim_{x\to \infty}\frac{2x+7}{x+8686} \end{equation*} $ </latex>

Intuicyjnie, jeśli x urośnie do odpowiednio dużej liczby, stałe czynniki staną się nieistotne i góra oraz dół ułamka będą zdominowane przez czynniki 2x i x, dając wynik dążący do 2.

Jednym sposobem sprawdzenia tego jest podzielenie góry i dołu ułamka przez x otrzymując:

<latex> $ \begin{equation*} \frac{2+\frac{7}{x}}{1+\frac{8686}{x}} \end{equation*} $ </latex>

Jeśli x jest nieskończone, to standardowa część górnej części ułamka to 2, a dolnej 1, więc standardowa część całości wynosi 2.

Innym podejście, byłoby zastosowanie reguły de l'Hospitala. Pochodna góry wynosi 2, dołu 1, więc granica to 2/1=2. ++++